Thin elastic ribbons represent a class of intermediary objects lying in-between thin elastic plates and thin elastic rods. Although the two latter families of thin structures have received much interest from the Computer Graphics community over the last decades, ribbons have seldom been considered and modelled numerically so far, in spite of a growing number of applications in Computer Design.
In this paper, starting from the reduced developable ribbon models recently popularised in Soft Matter Physics, we propose a both accurate and efficient algorithm for computing the statics of a thin elastic ribbon. Inspired by the super-clothoid model for thin elastic rods, our method relies on compact ribbon elements whose normal curvature varies linearly with respect to arc length s, while their geodesic torsion is quadratic in s. In contrast however, for the sake of efficiency our algorithm avoids building a fully reduced kinematic chain and instead treats each element independently, gluing them only at the final solving stage through well-chosen bilateral constraints.
Thanks to this mixed variational strategy, which yields a banded Hessian, our algorithm recovers the linear complexity of low-order models while preserving the quadratic convergence of curvature-based models. As a result, our approach is scalable to a large number of elements, and suitable for various boundary conditions and unilateral contact constraints, making it possible to handle challenging scenarios such as confined buckling experiments or Möbius bands with contact. Remarkably, our mixed algorithm proves an order of magnitude faster compared to Discrete Element Ribbon models of the literature while achieving, in a few seconds only, high accuracy levels that remain out of reach for such low-order models. Additionally, our numerical model can incorporate various ribbon energies, including the Ribext model for quasi-developable ribbons recently introduced in Physics, which allows to transition smoothly between a rectangular Kirchhoff rod and a (developable) Sadowsky ribbon. Our numerical scheme is carefully validated against demanding experiments of the Physics literature, which demonstrates its accuracy, efficiency, robustness, and versatility.
Our MERCI code is publicly available at https://gitlab.inria.fr/elan-public-code/merci for the sake of reproducibility and future benchmarking.
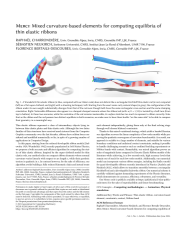 mixedribbonsTOG.pdf (5.45 Mo)
Télécharger le fichier
mixedribbonsTOG.pdf (5.45 Mo)
Télécharger le fichier
 teaserLeft.jpg (76.94 Ko)
Télécharger le fichier
tog-mixed-ribbons.mp4 (12.02 Mo)
Télécharger le fichier
teaserLeft.jpg (76.94 Ko)
Télécharger le fichier
tog-mixed-ribbons.mp4 (12.02 Mo)
Télécharger le fichier



