Polynomial identities involving Pascal's triangle rows
Résumé
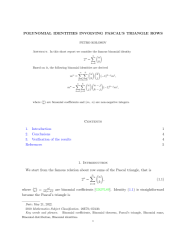
In this short report we consider the famous binomial identity
2n=n∑k=0(nk)
Based on it, the following binomial identities are derived
mn=n∑k=0k∑j=0(nk)(kj)(−1)k−jmj,mn=n∑k=0k∑j=0(nj)(n−jk−j)(−1)k−jmj,
where (nk) are binomial coefficients and (m, n) are non-negative integers.
Fichier principal
 PolynomialIdentitiesInvolvingPascalsTriangleRows.pdf (276.22 Ko)
Télécharger le fichier
PolynomialIdentitiesInvolvingPascalsTriangleRows.pdf (276.22 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|



