Uniform $C^{1,\alpha}$-regularity for almost-minimizers of some nonlocal perturbations of the perimeter
Résumé
In this paper, we establish a $C^{1,\alpha}$-regularity theorem for almost-minimizers of a functional $\mathcal{F}_{\varepsilon,\gamma}=P-\gamma P_{\varepsilon}$, where $\gamma\in (0,1)$ and $P_{\varepsilon}$ is a nonlocal energy converging to the perimeter as $\varepsilon$ vanishes. Our theorem provides a criterion for $C^{1,\alpha}$-regularity at a point of the boundary, which is uniform as the parameter $\varepsilon$ goes to $0$. Building upon previous work by the last two authors, as an application of this theorem we obtain that volume-constrained global minimizers of $\mathcal{F}_{\varepsilon,\gamma}$ are balls for any $\varepsilon$ small enough. For small $\varepsilon$, this minimization problem corresponds to the large mass regime for a Gamow-type problem where the nonlocal repulsive term is given by an integrable kernel $G$ with sufficiently fast decay at infinity.
Fichier principal
 uniform_regularity_hal1.pdf (749.77 Ko)
Télécharger le fichier
uniform_regularity_hal1.pdf (749.77 Ko)
Télécharger le fichier
 fig1.pdf (31.23 Ko)
Télécharger le fichier
fig1.pdf (31.23 Ko)
Télécharger le fichier
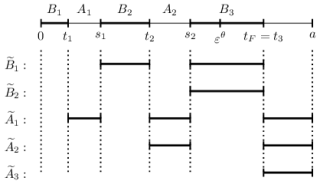 fig1b.pdf (41.29 Ko)
Télécharger le fichier
fig1b.pdf (41.29 Ko)
Télécharger le fichier
 fig2.pdf (31.27 Ko)
Télécharger le fichier
fig2.pdf (31.27 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |