Periodic solutions of a two-degree-of-freedom autonomous vibro-impact oscillator with sticking phases
Résumé
This contribution explores the free dynamics of a simple two-degree-of-freedom vibro-impact oscillator. One degree-of-freedom is limited by the presence of a rigid obstacle and periodic solutions involving one sticking phase per period (1-SPP) are targeted. A method to obtain such orbits is proposed: it provides conditions on the existence of 1-SPP as well as closed form solutions. It is shown that 1-SPP might not exist for a given combination of masses and stiffnesses. The set of 1-SPP is at most a countable set of isolated periodic orbits. The construction of 1-SPP requires numerical developments that are illustrated on a few relevant examples. Comparison with nonlinear modes of vibration involving one impact per period (1-IPP) is also considered. Interestingly, an equivalence between 1-SPP and a special set of isolated 1-IPP is established. It is also demonstrated that the prestressed system features sticking phases of infinite duration.
A few SPP orbits are animated below (click right -> view image for optimal quality).
Simplest SPP
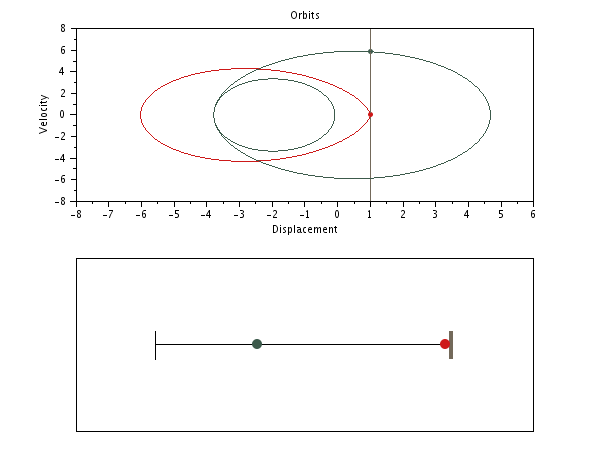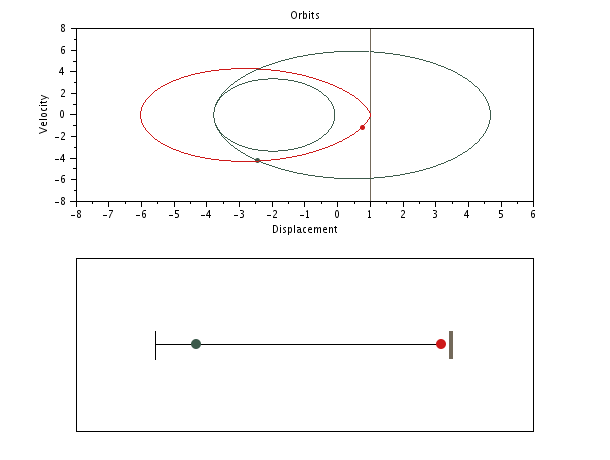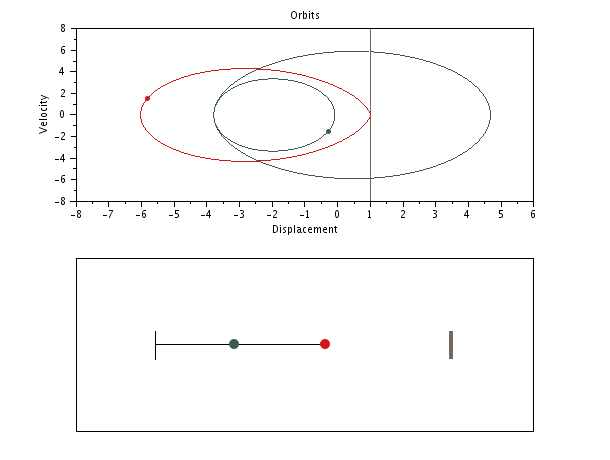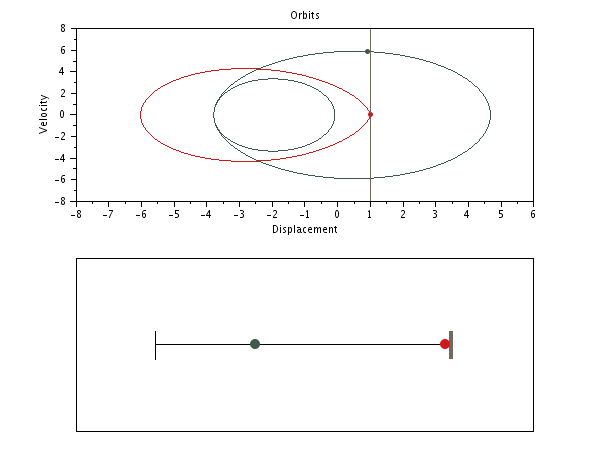 SPP with distinct masses but same stiffnesses
SPP with distinct masses but same stiffnesses
 SPP with same masses but distinct stiffnesses
SPP with same masses but distinct stiffnesses
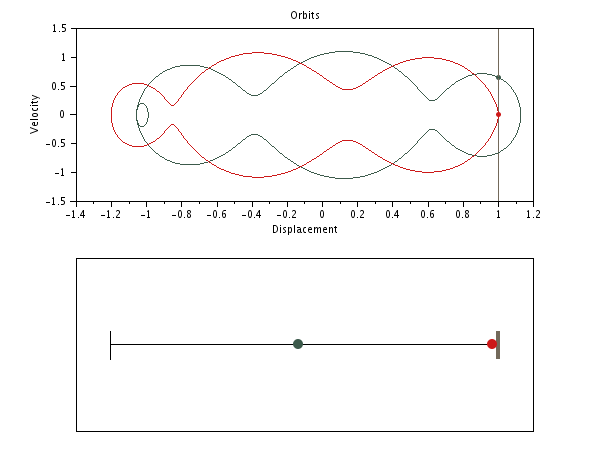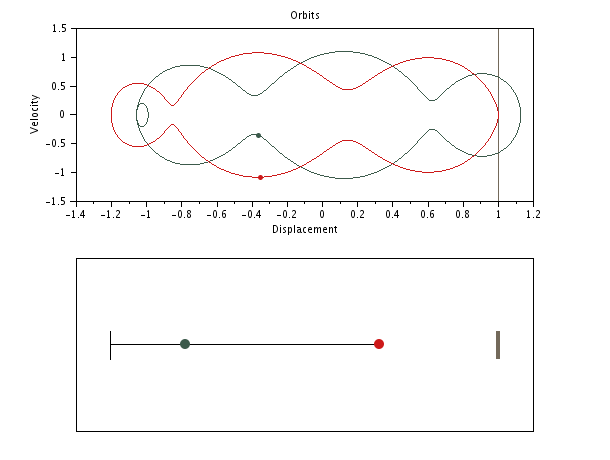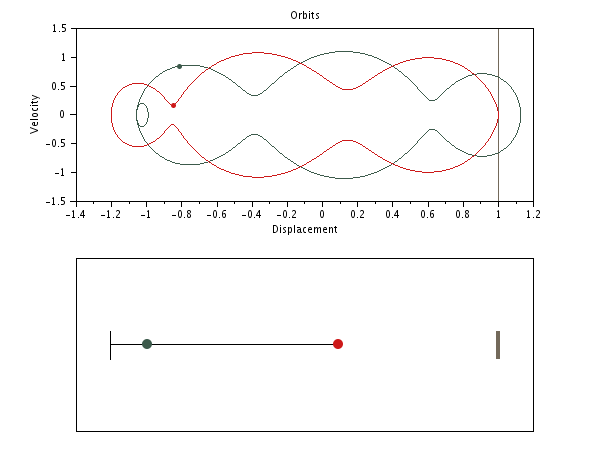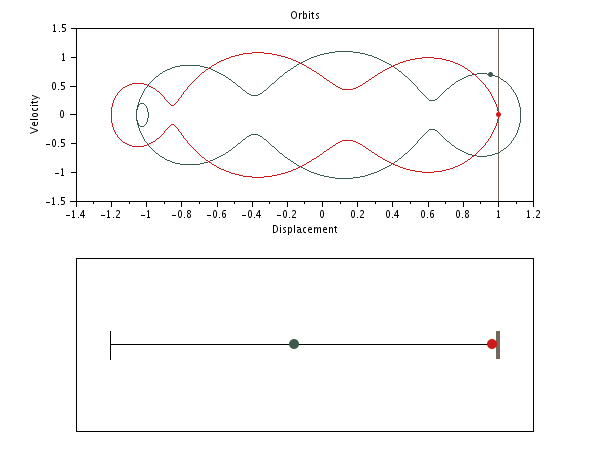 SPP with initial negative gap: sticking phase of infinite duration
SPP with initial negative gap: sticking phase of infinite duration
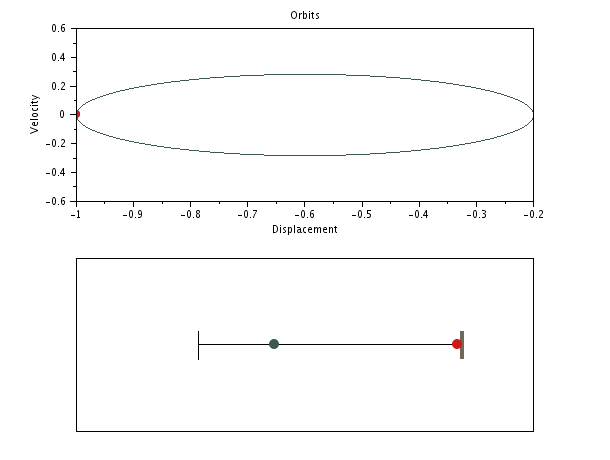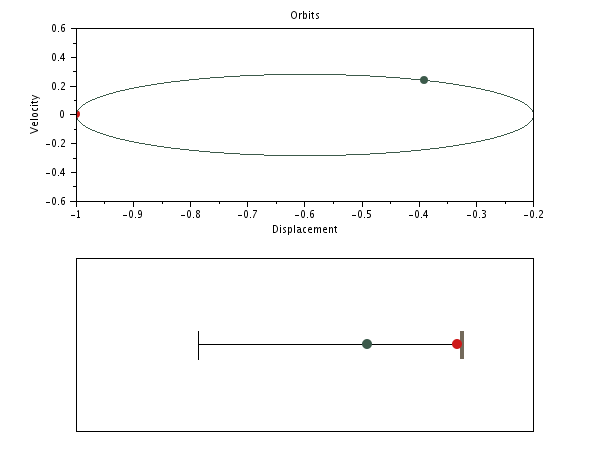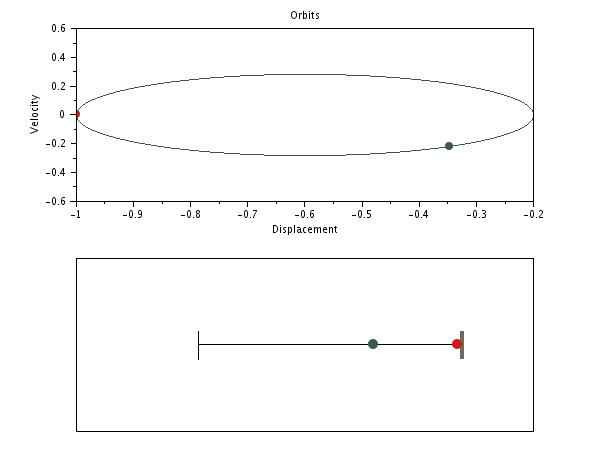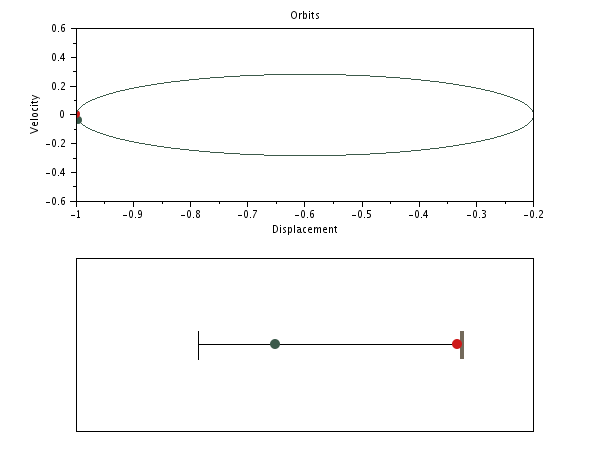
 SPP with distinct masses but same stiffnesses
SPP with distinct masses but same stiffnesses
 SPP with same masses but distinct stiffnesses
SPP with same masses but distinct stiffnesses
 SPP with initial negative gap: sticking phase of infinite duration
SPP with initial negative gap: sticking phase of infinite duration

Fichier principal
 LTJL.pdf (817.04 Ko)
Télécharger le fichier
LateX.zip (8.23 Mo)
Télécharger le fichier
scripts.zip (125.99 Ko)
Télécharger le fichier
LTJL.pdf (817.04 Ko)
Télécharger le fichier
LateX.zip (8.23 Mo)
Télécharger le fichier
scripts.zip (125.99 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
Loading...


