Folding optimal polygons from squares
Résumé
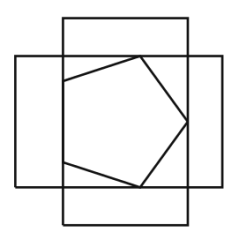
What is the largest regular n-gon that fits in a unit square? Can it be folded from a square piece of paper using standard moves from origami? Answering the first question is relatively easy, using simple ideas from geometry. The second is more interesting; our answer illustrates the difference between origami and the standard compass-and-straightedge constructions of the Greeks, where, for instance, the 7-gon cannot be constructed. Not only can we fold a 7-gon, but we can fold the largest one possible from a given square piece of paper.
The rotating caliper to design optimal bounding boxes:
The rotating caliper to design optimal bounding boxes:

Fichier principal
 preprint.pdf (278.22 Ko)
Télécharger le fichier
preprint.pdf (278.22 Ko)
Télécharger le fichier
 animation.gif (811.72 Ko)
Télécharger le fichier
AdditionalComments.pdf (91.74 Ko)
Télécharger le fichier
animation.gif (811.72 Ko)
Télécharger le fichier
AdditionalComments.pdf (91.74 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
| Commentaire | Principe de la recherche de l'enveloppe optimale dans le cas du pentagone. |
| Format | Autre |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
| Commentaire | Additional comments to the original paper |
Loading...


