Hamiltonian reduction using a convolutional auto-encoder coupled to an Hamiltonian neural network
Résumé
The reduction of Hamiltonian systems aims to build smaller reduced models, valid over a certain range of time and parameters, in order to reduce computing time. By maintaining the Hamiltonian structure in the reduced model, certain long-term stability properties can be preserved. In this paper, we propose a non-linear reduction method for models coming from the spatial discretization of partial differential equations: it is based on convolutional auto-encoders and Hamiltonian neural networks. Their training is coupled in order to simultaneously learn the encoder-decoder operators and the reduced dynamics. Several test cases on non-linear wave dynamics show that the method has better reduction properties than standard linear Hamiltonian reduction methods.
Fichier principal
 main.pdf (2.45 Mo)
Télécharger le fichier
main.pdf (2.45 Mo)
Télécharger le fichier
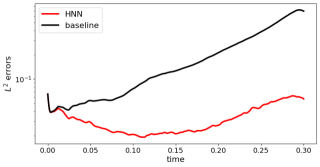 baseline_l2_errors_log.png (32.17 Ko)
Télécharger le fichier
autoencoder.png (824.98 Ko)
Télécharger le fichier
baseline_hnn_H_plot.png (41.07 Ko)
Télécharger le fichier
baseline_plot.png (234.04 Ko)
Télécharger le fichier
blueprint.png (79.73 Ko)
Télécharger le fichier
k1_test3_ae_hnn_wave_linear.png (162.54 Ko)
Télécharger le fichier
k1_test3_reduced_hami_wave_linear.png (29.87 Ko)
Télécharger le fichier
k24_test2_psd_shallow_water.png (132.34 Ko)
Télécharger le fichier
k3_test3_reduced_hami_wave_nonlinear.png (38.09 Ko)
Télécharger le fichier
k4_test2_ae_hnn_shallow_water.png (133 Ko)
Télécharger le fichier
k4_test2_psd_shallow_water.png (158.29 Ko)
Télécharger le fichier
k4_test3_reduced_hami_shallow_water.png (32.54 Ko)
Télécharger le fichier
k6_test3_psd_wave_linear.png (149.48 Ko)
Télécharger le fichier
loss_train_val_step_1.png (101.81 Ko)
Télécharger le fichier
loss_train_val_step_2.png (118.89 Ko)
Télécharger le fichier
shallow_water_final_condition.png (130.66 Ko)
Télécharger le fichier
shallow_water_initial_condition.png (67.15 Ko)
Télécharger le fichier
wave_linear_final_condition.png (153.59 Ko)
Télécharger le fichier
wave_non_linear_final_condition.png (137.97 Ko)
Télécharger le fichier
wave_non_linear_initial_condition.png (52.39 Ko)
Télécharger le fichier
baseline_l2_errors_log.png (32.17 Ko)
Télécharger le fichier
autoencoder.png (824.98 Ko)
Télécharger le fichier
baseline_hnn_H_plot.png (41.07 Ko)
Télécharger le fichier
baseline_plot.png (234.04 Ko)
Télécharger le fichier
blueprint.png (79.73 Ko)
Télécharger le fichier
k1_test3_ae_hnn_wave_linear.png (162.54 Ko)
Télécharger le fichier
k1_test3_reduced_hami_wave_linear.png (29.87 Ko)
Télécharger le fichier
k24_test2_psd_shallow_water.png (132.34 Ko)
Télécharger le fichier
k3_test3_reduced_hami_wave_nonlinear.png (38.09 Ko)
Télécharger le fichier
k4_test2_ae_hnn_shallow_water.png (133 Ko)
Télécharger le fichier
k4_test2_psd_shallow_water.png (158.29 Ko)
Télécharger le fichier
k4_test3_reduced_hami_shallow_water.png (32.54 Ko)
Télécharger le fichier
k6_test3_psd_wave_linear.png (149.48 Ko)
Télécharger le fichier
loss_train_val_step_1.png (101.81 Ko)
Télécharger le fichier
loss_train_val_step_2.png (118.89 Ko)
Télécharger le fichier
shallow_water_final_condition.png (130.66 Ko)
Télécharger le fichier
shallow_water_initial_condition.png (67.15 Ko)
Télécharger le fichier
wave_linear_final_condition.png (153.59 Ko)
Télécharger le fichier
wave_non_linear_final_condition.png (137.97 Ko)
Télécharger le fichier
wave_non_linear_initial_condition.png (52.39 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |