Improved Routing on the Delaunay Triangulation
Résumé
A geometric graph G = (P,E) is a set of points in the plane and edges between pairs of points,
where the weight of the edge is equal to the Euclidean distance between the points. In k-local
routing we find a path through G from a source vertex s to a destination vertex t, using only
knowledge of the present location, the locations of s and t, and the k-neighbourhood of the
current vertex. We present an algorithm for 1-local routing on the Delaunay triangulation, and
show that it finds a path between a source vertex s and a target vertex t that is not longer than
3.56|st|, improving the previous bound of 5.9.
Fichier principal
 bestchord.pdf (1.35 Mo)
Télécharger le fichier
bestchord.pdf (1.35 Mo)
Télécharger le fichier
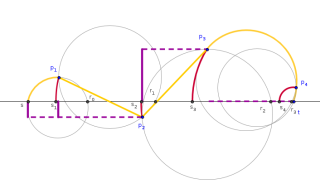 exampleRouting.png (36.78 Ko)
Télécharger le fichier
exampleRouting.png (36.78 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
Loading...