 |
 |
\(\mathrm{Nicolas\ Baca\ddot{e}r}\)
\(\mathrm{Institut\ de\ Recherche\ pour\ le\ D\acute{e}veloppement}\)
Unité de modélisation mathématique et informatique des systèmes complexes
Les Cordeliers, Paris, France
nicolas.bacaer@ird.fr
On ajuste un modèle épidémique de type S-E-I-R aux données épidémiques du nouveau coronavirus en France en 2020. Si les contacts sont réduits à zéro à partir d'une certaine date proche du début de l'épidémie, la taille finale de l'épidémie est proche de celle que l'on obtient en multipliant le nombre cumulés de cas à cette date par la reproductivité \(\mathcal{R}_0\) de l'épidémie. Avec nos estimations, \(\mathcal{R}_0\simeq \mbox{2,3}\) en France.
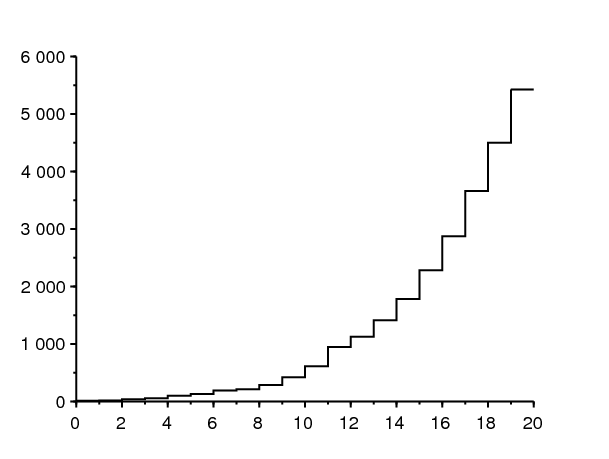
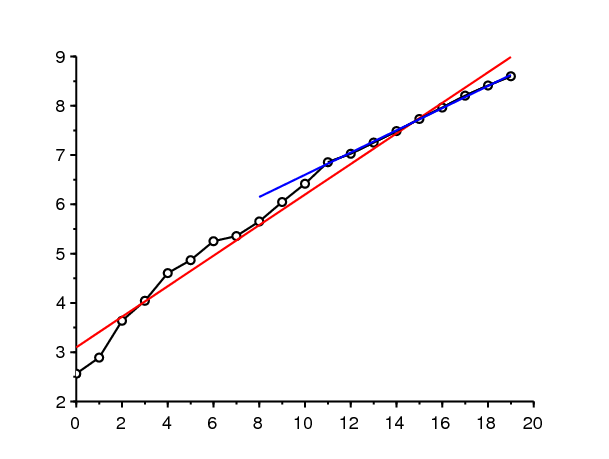
La figure 1\(^a\) montre le nombre cumulé de cas détectés de coronavirus en France entre le 25 février et le 15 mars 2020. Entre ces deux dates, le nombre cumulé est passé de 13 à 5427. On observe une croissance qui a l'air exponentielle. La figure 1\(^b\) montre comment une droite de régression s'ajuste en coordonnées logarithmiques. On trouve que la courbe croît comme \(e^{\lambda t}\) avec un taux de croissance \(\lambda \simeq 0,31\) par jour (droite rouge). Le temps de doublement est \(\log(2)/\lambda \simeq \mbox{2,2}\) jours. Si en revanche on se limite aux 9 derniers jours, qui sont particulièrement bien alignés en échelle logarithmique, on obtient \(\lambda \simeq 0,225\) par jour et un temps de doublement de \(\mbox{3,1}\) jours (droite bleue). Comme les données du début de l'épidémie sont perturbées par une part importante de nouveaux cas qui sont importés, c'est probablement la deuxième estimation qui est plus fiable ; c'est celle que nous utiliserons ci-dessous.


Proposons un modèle mathématique pour cette épidémie. Divisons la population française en quatre compartiments selon le modèle classique S-E-I-R (voir par exemple [2,p. 61]) : susceptible d'être infecté (\(S\)), infecté mais non infectieux (\(E\)), infectieux sans protection (\(I\)) et non susceptible de transmettre l'infection (c'est-à-dire infectieux mais confiné, guéri ou décédé, \(R\)). On peut évidemment raffiner à l'infini ce modèle pour le rendre plus réaliste (voir par exemple parmi de nombreuses autres références [3,7]) mais on a essayé de limiter au maximum le nombre de paramètres inconnus ; on a aussi pour but d'obtenir un résultat plus d'ordre théorique que pratique.
Notons \(N\) la population totale, \(a\) le taux de contact effectif, \(b\) le taux auquel les personnes infectées deviennent infectieuses et \(c\) le taux auquel les personnes infectieuses sont isolées : \begin{eqnarray} \frac{dS}{dt} &=& -a\, S\, \frac{I}{N}\tag{1}\\ \frac{dE}{dt} &=& a\, S\, \frac{I}{N} - b\, E\tag{2}\\ \frac{dI}{dt} &=& b\, E - c\, I\tag{3}\\ \frac{dR}{dt} &=& c\, I,\tag{4} \end{eqnarray} avec \(N=S(t)+E(t)+I(t)+R(t)\). Pour faire le lien avec les données, on peut penser que \(R(t)\) correspond au nombre cumulé de cas connus à l'instant \(t\).
Au début de l'épidémie, le nombre de cas reste très petit par rapport à la population totale de sorte que \(S(t)\simeq N\), ce qui conduit à la linéarisation \[ \frac{dE}{dt} \simeq a\, I - b\, E,\quad \quad \frac{dI}{dt} \simeq b\, E - c\, I. \] L'épidémie tend donc à croître exponentiellement comme \(e^{\lambda t}\), où \(\lambda\) est la plus grande valeur propre de la matrice \begin{equation}\tag{5} \left (\begin{array}{cc} -b & a\\ b & -c \end{array} \right ). \end{equation} Le polynôme caractéristique est \begin{equation}\tag{6} \lambda^2 +(b+c)\lambda +b(c-a)=0. \end{equation} Donc \begin{equation}\tag{7} \lambda=\frac{-(b+c)+\sqrt{(b+c)^2-4b(c-a)}}{2} = \frac{-(b+c)+\sqrt{(b-c)^2+4ab}}{2}\, . \end{equation} La durée moyenne dans le compartiment \(E\), qui vaut \(1/b\) et que l'on assimile à la période d'incubation, serait de l'ordre de 4 jours [4]. Prenons par conséquent \(b= \mbox{0,25}\) par jour. La durée moyenne dans le compartiment \(I\) avant isolement, qui vaut \(1/c\), est plus difficile à estimer car elle dépend non seulement des caractéristiques biologiques du virus mais aussi de la promptitude avec laquelle les cas sont isolés, ce qui varie d'un pays à l'autre. Supposons qu'elle soit de l'ordre de 1 jour puisque l'épidémie en France a lieu alors que les habitants sont déjà bien au courant de l'existence de la pandémie ; les malades ne tardent pas à \^etre isolés. Ainsi \(c= 1\) par jour. On déduit de la formule (7) que \begin{equation}\tag{8} a = \frac{(2\lambda+b+c)^2-(b-c)^2}{4b}=(\lambda+c)\left (1+\frac{\lambda}{b}\right ). \end{equation} ce qui permettrait de calculer numériquement le taux de contact effectif \(a\) à partir du taux de croissance observé \(\lambda\).
Imaginons que des mesures de santé publique puissent diviser le taux de contact effectif par un nombre \(k\) qui soit supérieur à 1. Combien doit valoir au minimum \(k\) pour arrêter l'épidémie ? Cette valeur de \(k\), traditionnellement notée \(\mathcal{R}_0\) à la suite de Lotka et appelée par lui « reproductivité » [8, p. 102], s'obtient simplement en remarquant que lorsque \(a\) est remplacé par \(a'=a/\mathcal{R}_0\), le nouveau taux de croissance de l'épidémie \(\lambda'\) doit être nul, ce qui d'après l'équation (6) conduit à \(c- a/\mathcal{R}_0=0\) et à \[ \mathcal{R}_0 = \frac{a}{c}=\left (1+\frac{\lambda}{b}\right ) \left (1+\frac{\lambda}{c}\right ) \simeq \mbox{2,33}\] si l'on utilise la valeur numérique (\(\lambda\simeq \mbox{0,225}\) par jour) suggérée par la courbe épidémique de la figure 1. Vues les incertitudes sur les paramètres \(b\) et \(c\), ceci ne peut être qu'une valeur approchée.
De manière plus technique (voir par exemple [9]), on aurait pu remarquer que \(\mathcal{R}_0\) était aussi le rayon spectral de la matrice \[\left (\begin{array}{cc} 0 & a \\ 0 & 0 \end{array} \right ) \left (\begin{array}{cc} b & 0 \\ -b & c \end{array} \right )^{-1}.\]
Revenons au modèle S-E-I-R (1)-(4). Rappelons comment déterminer la taille finale de l'épidémie en l'absence complète d'intervention ; c'est une adaptation facile de la méthode utilisée pour le modèle S-I-R (voir par exemple [6, p. 76]). L'équation (1) montre que \[\frac{d}{dt} \log S = -\frac{a}{N} I(t),\] donc en intégrant de \(t=0\) à \(t=+\infty\) : \begin{equation}\tag{9} \log S(\infty) - \log S(0) = -\frac{a}{N} \int_0^\infty I(t)\, dt\, . \end{equation} Au début de l'épidémie, personne n'est encore dans le compartiment \(R\), donc \(R(0)=0\). L'équation (4) montre que \begin{equation}\tag{10} R(\infty) = c\int_0^\infty I(t)\, dt, \end{equation} où \(R(\infty)\) désigne la limite quand \(t\to +\infty\) de la fonction \(R(t)\), qui est croissante et majorée par \(N\). Par ailleurs, on a à tout instant \(S(t)+E(t)+I(t)+R(t)=N\). Quand \(t \to +\infty\), l'épidémie finit par s'arrêter de sorte que \(E(t)\) et \(I(t)\) tendent vers 0. À la limite, il ne reste donc que les personnes qui ont échappé à l'épidémie et celles qui ont été infectées mais qui sont passées dans le compartiment \(R\) : \begin{equation}\tag{11} S(\infty)+R(\infty)=N. \end{equation} En combinant (9), (10) et (11), on voit que \[N-R(\infty)=S(0)\, \exp\left (-\frac{a}{c} \frac{R(\infty)}{N} \right ).\] Au début de l'épidémie, il n'y a que quelques personnes infectées dans la population, donc \(S(0)\simeq N\). L'équation pour la taille finale de l'épidémie peut s'écrire comme \[1-\frac{R(\infty)}{N} \simeq \exp\left (-\mathcal{R}_0 \, \frac{R(\infty)}{N}\right ),\] qui se trouve avoir la même forme que pour le modèle S-I-R [6]. Avec \(\mathcal{R}_0\simeq \mbox{2,33}\), on trouve numériquement \(R(\infty)/N \simeq 87\%\).
Imaginons qu'à une certaine date \(\tau\), des mesures drastiques soient prises de sorte que le nouveau taux de contact effectif soit réduit à 0 alors qu'il y a \(R(\tau)\) cas cumulés. Par exemple, il y avait 5427 cas cumulés au 15 mars, date à laquelle sont entrées en vigueur les mesures concernant les écoles et les lieux publics [5]. Peut-on alors prévoir quelle sera la nouvelle taille finale de l'épidémie ?
Vers la fin de la phase exponentielle où \(t\leq \tau\) et où le nombre total de cas représente encore une part infime de la population totale, on a \[E(t)\simeq u\, e^{\lambda t},\quad I(t)\simeq v\, e^{\lambda t},\quad R(t)\simeq w\, e^{\lambda t},\] où \((u,v)\) est un vecteur propre associé à la plus grande valeur propre \(\lambda\) de la matrice (5). Ainsi, \(-b\, u+a\, v=\lambda \, u\). Avec l'équation (8), on trouve que \[u=\frac{a\, v}{\lambda+b}=\frac{\lambda+c}{b}\, v\, .\] Comme \(dR/dt \simeq \lambda R\) pour \(t < \tau\) lorsque \(t\) n'est pas trop proche de 0, on a \[I(\tau)=\frac{1}{c} \frac{dR}{dt}(\tau)\simeq \frac{\lambda }{c}\, R(\tau).\] Mais \(I(\tau)\simeq v\, e^{\lambda \tau}\), donc \[E(\tau)\simeq u\, e^{\lambda \tau} = \frac{\lambda+c}{b}\, v\, e^{\lambda \tau} \simeq \frac{\lambda+c}{b}\, I(\tau) \simeq \left (\frac{\lambda^2}{bc}+ \frac{\lambda }{b}\right ) R(\tau) \, .\]
Les contacts étant supposés réduits à zéro, on a pour \(t > \tau\) \begin{eqnarray} \frac{dS}{dt} &=& 0\tag{12}\\ \frac{dE}{dt} &=& - b\, E\tag{13}\\ \frac{dI}{dt} &=& b\, E - c\, I\tag{14}\\ \frac{dR}{dt} &=& c\, I.\tag{15} \end{eqnarray} Sans avoir à résoudre ce système, il est clair que la taille finale de l'épidémie sera \(R(\infty)=R(\tau)+E(\tau)+I(\tau)\), puisqu'il y a \(E(\tau)+I(\tau)\) individus infectés qui ne sont pas encore dans le compartiment \(R\) au temps \(\tau\). Ainsi \[R(\infty)\simeq R(\tau) \left (1+\frac{\lambda^2}{bc}+ \frac{\lambda }{b}+ \frac{\lambda}{c}\right ) = R(\tau) \left (1+\frac{\lambda}{b} \right ) \left (1+\frac{\lambda}{c} \right )=\mathcal{R}_0 \, R(\tau) \, .\] Ainsi, si les contacts sont réduits à zéro à partir d'une certaine date proche du début de l'épidémie (assez proche pour que l'approximation linéaire soit encore valable mais pas trop proche pour que le système linéarisé ait eu le temps de converger vers le vecteur propre associé à la première valeur propre), alors la taille finale de l'épidémie est proche de celle que l'on obtient en multipliant le nombre cumulés de cas à cette date par la reproductivité \(\mathcal{R}_0\) de l'épidémie. Un pareil résultat s'obtient facilement de la même manière pour un modèle S-I-R. Mais le degré de généralité de cette observation reste à déterminer.
Notons au passage l'analogie avec le concept de « potentiel d'accroissement » des populations en démographie [10, p. 176]. C'est le rapport entre la population finale stationnaire et la population à un certain instant si la fertilité est divisée subitement à cet instant par la reproductivité \(\mathcal{R}_0\), de sorte que la population se retrouve avec un taux asymptotique de croissance nul. Comme dans notre calcul, c'est en supposant que la population initiale est « stable » au sens de Lotka (c'est-à-dire donnée par le premier vecteur propre) que Keyfitz a obtenu une formule relativement simple pour le potentiel d'accroissement, formule qui fait aussi intervenir \(\mathcal{R}_0\) quoique de manière plus compliquée que pour notre modèle S-E-I-R [10, p. 179].
Notons aussi que l'estimation de \(R(\tau)+E(\tau)+I(\tau)\) à partir de la donnée \(R(\tau)\) seule est analogue au problème qui s'était posé aux débuts de l'épidémie de VIH pour estimer le nombre de personnes séropositives à partir du nombre de cas déclarés de SIDA.
Avec \(R(\tau)=5427\) et \(\mathcal{R}_0\simeq \mbox{2,33}\), cela donne \(R(\infty)\simeq 12\, 600\). Soulignons encore une fois l'incertitude autour des paramètres \(b\) et \(c\), qui se retrouve dans la valeur de \(R(\infty)\).
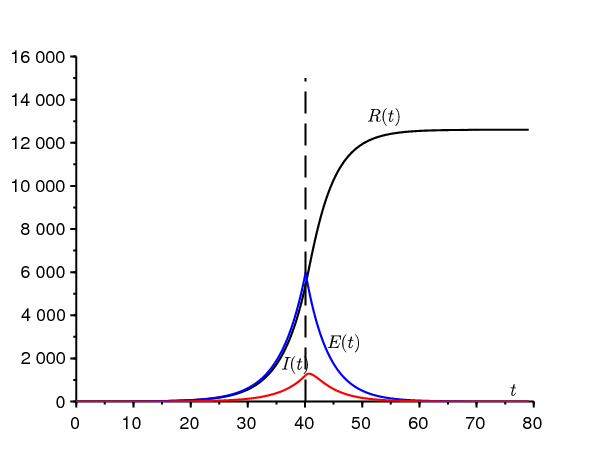
La figure 2\(^a\) illustre ce modèle à deux phases. On a pris \(N=65\times 10^6\), \(S(0)=N-1\), \(E(0)=1\), \(I(0)=0\) et \(R(0)=0\). Le paramètre \(a\) est donné par la formule (8) avec \(\lambda=\mbox{0,225}\) par jour. On a pris \(\tau=\mbox{40,1}\) jours de sorte que \(R(\tau) \simeq 5415\) soit très proche de la donnée 5427 du 15 mars. En poursuivant la simulation un peu plus longtemps que dans la figure, on trouve bien numériquement que \(R(\infty)/R(\tau)\simeq \mbox{2,33} \simeq \mathcal{R}_0\).

Dans la réalité, le taux de contact effectif ne sera sûrement pas tout à fait nul pour \(t > \tau\). La valeur obtenue pour \(R(\infty)\) peut néanmoins être considérée comme une borne inférieure de la valeur réelle puisqu'il est certain que la taille finale de l'épidémie sera supérieure avec des contacts non nuls qu'avec des contacts nuls pour \(t > \tau\). Rappelons à ce sujet que les modèles épidémiques de type S-I-R ou S-E-I-R avec un taux de contact variable ne sont pas « monotones », dans le sens qu'une réduction du taux de contact peut parfois conduire à une taille finale de l'épidémie plus grande [1].
Si l'on veut savoir quand aura lieu le pic d'arrivée de nouveaux cas, ce qui peut avoir son importance pour les problèmes de congestion dans les hôpitaux, il faut résoudre le système (12)-(15). On trouve \(E(t)=E(\tau)\, e^{-b(t-\tau)}\) et \begin{eqnarray*} I(t) &=& I(\tau) e^{-c(t-\tau)} + b\int_\tau^t e^{-c(t-s)} E(s)\, ds\\ &=& I(\tau) e^{-c(t-\tau)} + b E(\tau)\, \frac{e^{-b(t-\tau)}-e^{-c(t-\tau)}}{c-b}\ . \end{eqnarray*} Avec les valeurs numériques de la figure 2\(^a\), on a \(E(\tau)\simeq 5\,970\), \(I(\tau)\simeq 1\,218\) et la dérivée de \(I(t)\) s'annule 0,6 jours après que le taux de contact a été ramené à 0. Pour un taux de contact non nul, le délai serait évidemment plus long.
En conclusion, on a exploré le scénario le plus favorable, celui où le taux de contact est réduit à zéro à partir d'un certaine date. On a trouvé une formule approchée simple pour la taille finale de l'épidémie en fonction du nombre de cas détectés au moment de la réduction. Il reste néanmoins à énoncer et à démontrer plus rigoureusement ce résultat, sans doute en faisant tendre la population totale \(N\) vers \(+\infty\).
On remercie Hisashi Inaba et Ali Moussaoui pour leurs commentaires sur le manuscrit.