\(^1\) Unité de modélisation mathématique et informatique des systèmes complexes, Institut de recherche pour le développement,
Les Cordeliers, Paris, France, nicolas.bacaer@ird.fr
\(^2\) Nice, France, lobrinria@wanadoo.fr
\(^3\) ITAP, Université de Montpellier, INRAE, Institut Agro, Montpellier, France, tewfik.sari@irstea.fr
On s'intéresse à la probabilité d'extinction d'un processus linéaire de naissance et de mort avec plusieurs types dans un environnement périodique quand la période des coefficients est très grande. Cette probabilité peut présenter à la limite une discontinuité en lien avec un canard dans un système dynamique lent-rapide. On détermine précisément le point de discontinuité dans un exemple avec deux types d'individus.
Mots clés : processus de naissance et de mort, environnement périodique, système lent-rapide
L'estimation de la probabilité d'extinction d'une population est une question qui intervient notamment en biologie de la conservation et en épidémiologie. Dans ce deuxième cas, par population il faut entendre population infectée. Un modèle mathématique classique pour étudier ce genre de problème est celui des processus linéaires de naissance et de mort avec un ou plusieurs types d'individus (Méléard, 2016). Il faut néanmoins tenir compte dans de nombreuses situations de la saisonnalité de l'environnement, ce qui conduit à l'étude de ces processus lorsque les coefficients de naissance et de mort sont des fonctions périodiques du temps (Bacaër et Ait Dads, 2014). Certaines populations ou certaines épidémies ont des coefficients dont l'échelle de temps est relativement courte par rapport à la saisonnalité annuelle ; on est donc amené à considérer la limite où la période des coefficients est très grande. Lorsque les paramètres vitaux sont sous-critiques pendant une partie de l'année (la saison défavorable), la probabilité d'extinction comme fonction de la saison de démarrage du processus converge vers une limite discontinue (Carmona et Gandon, 2019). Le point de discontinuité se trouve avant le début de la saison défavorable.
Bacaër (2019) avait poursuivi cette étude essentiellement dans le cas d'un seul type d'individus, en remarquant notamment que la discontinuité de la probabilité d'extinction était liée à la présence dans un système dynamique lent-rapide d'un « canard », c'est-à-dire (voir par exemple Lobry (2018, chapitre 5)) d'une trajectoire qui longe un arc attractif pendant un certain temps avant de longer un arc répulsif. On se propose ci-dessous d'étudier un exemple avec deux types d'individus inspiré d'un modèle de transmission d'une maladie à vecteurs. On détermine précisément le point de discontinuité de la probabilité d'extinction. Ce problème était resté non résolu (Carmona et Gandon, 2019 ; Bacaër, 2019).
Dans la section 2, on présente le modèle pour la population, à savoir celui des processus linéaires de naissance et de mort à coefficients périodiques avec plusieurs types d'individus. On explique que la probabilité d'extinction est liée à un système d'équations différentielles ordinaires. Lorsque la période converge vers l'infini, un changement de variable transforme ce système en un système lent-rapide avec une période fixe.
Dans la section 3, on présente un exemple avec deux types d'individus. Des simulations numériques suggèrent que la probabilité d'extinction converge vers une limite discontinue et que le point de discontinuité est déterminé par une condition qui fait intervenir l'intégrale de la valeur propre dominante d'une certaine matrice. Dans la section 4, on démontre avec les outils de l'analyse non standard que c'est bien cette condition qui détermine le point de discontinuité. Dans la section 5, on présente un autre exemple avec cette fois quatre types d'individus. Une simulation numérique suggère qu'une condition du même type détermine encore le point de discontinuité. Nous ne sommes néanmoins pas parvenu à le démontrer dans un cadre général lorsque le nombre de types d'individus est strictement supérieur à deux.
On considère un processus linéaire de naissance et de mort avec k types (k≥1) dans un environnement périodique. T>0 est la période de l'environnement. On se donne deux fonctions matricielles \(\,A(t)=(A_{i,j}(t)) \) et \( B(t)=(B_{i,j}(t)) \) de taille k et de période T avec les hypothèses suivantes :
Plus précisément, comme dans (Bacaër et Ait Dads, 2014), on définit
On suppose qu'au temps \(t_0\) il y a \(n_i\geq 0\) individus de type i (les \(n_i\) sont des entiers, \(1\leq i \leq k\)) avec \(\sum_i n_i \geq 1\). On peut supposer que \(0\leq t_0 < T\). D'après (Bacaër et Ait Dads, 2014), la probabilité \(\,p(t_0,t_1)\) que la population soit éteinte à ce second instant, c'est-à-dire qu'il ne reste aucun individu des différents types, est donnée par \[p(t_0,t_1)=[z_1(t_1-t_0)]^{n_1}\cdots [z_k(t_1-t_0)]^{n_k},\quad \forall t_1>t_0.\] \(z(t)=(z_i(t))_{1\leq i \leq k}\) est la solution du système différentiel \[ \frac{dz_i}{dt}(t)=\sum_j [1-z_j(t)] [B_{j,i}(t_1-t)-A_{j,i}(t_1-t)z_i(t)] ,\quad 0 < t < t_1-t_0, \] avec la condition initiale \( z_i(0)=0 \ \forall i\).
L'espérance du nombre d'individus de type i au temps t est solution de \[\frac{dE_i}{dt} = \sum_j C_{i,j}(t)\, E_j(t)\] et \(E_i(t_0)=n_i\ \forall i\). On définit
On suppose
On définit
Si T converge vers +∞, autrement dit si \(\varepsilon \to 0\), le système (2.1) peut s'écrire comme un système autonome lent-rapide avec k variables rapides \(x_i(s)\) \((1\leq i\leq k)\) et une variable lente \(x_{k+1}(s)=s\) avec \(dx_{k+1}/ds=1\).
Pour la solution stationnaire triviale \(x_i=1\ \forall i\), la matrice jacobienne du membre de droite du système (2.1) est \(\tilde{c}(s_0+m-s)\). \(\tilde{c}\) désigne la matrice transposée de la matrice c. D'après un corollaire du théorème de Perron et Frobenius pour les matrices irréductibles dont les coefficients en dehors de la diagonale sont tous positifs ou nuls (Allaire et coll., 2018, remarque 6.2.13), les matrices \(c(s)\) et \(\tilde{c}(s)\) ont une valeur propre réelle dominante commune \(\Lambda(s)\), strictement supérieure à la partie réelle de toutes les autres valeurs propres.
Prenons \[a(s)=\left (\begin{array}{cc} 0 & \alpha(s) \\ \gamma & 0 \end{array}\right ) , \quad b(s)=\left (\begin{array}{cc} \beta & 0 \\ 0 & \delta \end{array}\right ),\] avec \(\alpha(s)>0\), \(\beta>0\), \(\gamma>0\) et \(\delta>0\). \(\alpha(s)\) est une fonction continue périodique de période 1. Ce modèle stochastique s'inspire du modèle déterministe linéarisé pour une maladie à vecteurs de (Bacaër, 2007, Section 4.1) : \begin{equation}\tag{3.1} \frac{dW}{dt} = \left (\begin{array}{cc} -\beta & \alpha(t/T) \\ \gamma & -\delta \end{array}\right )W=c(t/T)\, W. \end{equation} Les vecteurs infectés sont le type 1. Les personnes infectées sont le type 2. Le paramètre \(\alpha(s)\) est le taux auquel les personnes infectées transmettent leur infection à des vecteurs lorsqu'elles sont piquées. Ce taux est périodique car la population de vecteurs sains l'est aussi. Le paramètre β est le taux auquel les vecteurs meurent. Le paramètre γ est le taux auquel les vecteurs piquent. Le paramètre δ est le taux auquel les personnes infectées guérissent. Le système (2.1) s'écrit alors \begin{eqnarray} \varepsilon\, \frac{dx_1}{ds}(s)&=& \beta\, [1-x_1(s)] -\gamma \, x_1(s) [1-x_2(s)] , \tag{3.2}\\ \varepsilon\, \frac{dx_2}{ds}(s)&=& \delta\, [1-x_2(s)]- \alpha(s_0+m-s)\, [1-x_1(s)]\, x_2(s). \tag{3.3} \end{eqnarray} Notons que les membres de droite s'annulent dans deux cas : \(x_1(s)= 1\) et \(x_2(s)= 1\), ou bien \[ x_1(s) = {x}_1^*(s)= \frac{1+\frac{\delta}{\alpha(s_0+m-s) }}{1+\frac{\gamma}{\beta}}\quad ,\quad x_2(s) = {x}^*_2(s)= \frac{1+\frac{\beta}{\gamma}}{1+\frac{\alpha(s_0+m-s)}{\delta}}\, . \tag{3.4} \] Les deux valeurs propres de la matrice \(c(s)\) sont des nombres réels : \begin{eqnarray} \lambda_\pm(s) &=& \frac{-(\beta+\delta) \pm \sqrt{(\beta+\delta)^2 + 4 [\alpha(s) \gamma-\beta \delta]}}{2} \, .\tag{3.5} \end{eqnarray} La valeur propre dominante est \(\Lambda(s)=\lambda_+(s)\). On a \(\,\lambda_-(s) < 0\ \forall s\).
Supposons qu'il existe une saison défavorable à la transmission de l'épidémie, c'est-à-dire \( \exists \, 0 < s_1 < s_2 <1\) avec \begin{equation} \frac{\alpha(s)\, \gamma}{\beta \, \delta}<1\quad \Leftrightarrow \quad \Lambda(s)<0\quad \forall s\in ]s_1,s_2[, \tag{3.6} \end{equation} \begin{equation} \frac{\alpha(s)\, \gamma}{\beta \, \delta}>1\quad \Leftrightarrow \quad \Lambda(s)>0 \quad \forall s\in ]0,s_1[\cup ]s_2,1[. \tag{3.7} \end{equation} Supposons de plus que \begin{equation} \int_0^1 \Lambda(s)\, ds >0. \tag{3.8} \end{equation}
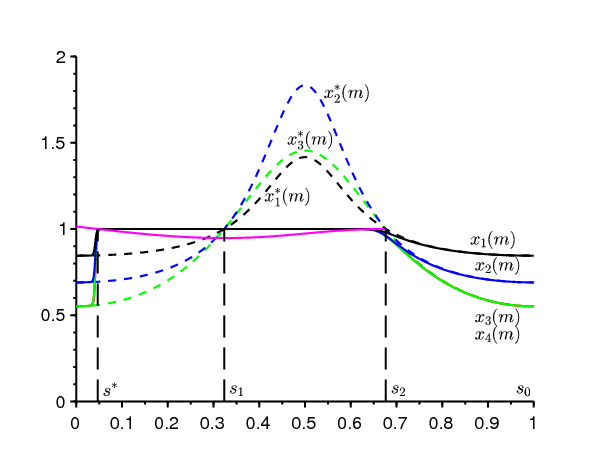
Comme exemple, prenons \(\alpha(s)=\bar{\alpha}(1+\kappa \cos (2\pi s))\) avec \(\bar{\alpha}>0\), \(|\kappa|<1\) et \[\frac{\bar{\alpha} (1-\kappa)\, \gamma}{\beta \, \delta}<1<\frac{\bar{\alpha} (1+\kappa)\, \gamma}{\beta \, \delta}.\] Cette dernière condition assure qu'il y a bien une saison défavorable. Plus spécifiquement, choisissons \(\,\bar{\alpha}=3\), \(\kappa=\mbox{0,75}\), \(\beta=2\), \(\gamma=1\) et \(\delta=1\). Ces valeurs ne sont pas très réalistes mais elles mettent bien en évidence le phénomène. On a alors \(s_1\simeq \mbox{0,323}\) et \(s_2\simeq \mbox{0,677}\). On peut vérifier numériquement que la condition (3.8) est vérifiée. Prenons par ailleurs \(T=1000\), \(m=3\) et \(s_0=\mbox{0,25}\). La figure 1 représente la solution du système (3.2)-(3.3) avec la condition initiale \(x_1(0)=x_2(0)=0\). On a utilisé le logiciel Scilab et résolu le système différentiel pour \(\log(1-x_1(s))\) et \(\log(1-x_2(s))\). Puis on est revenu aux variables initiales. On a également tracé la fonction constante égale à 1 et les courbes (3.4). Notons les choses suivantes :

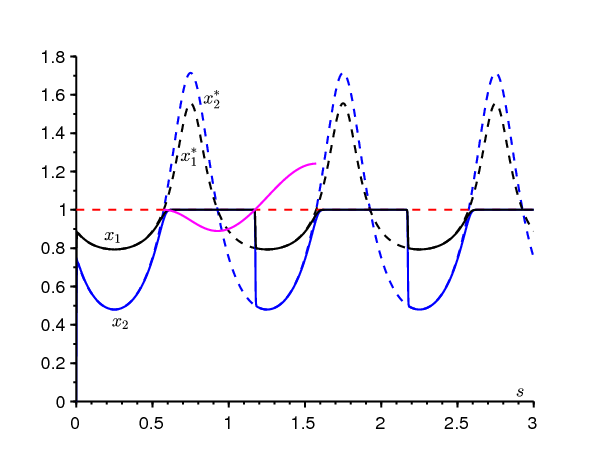
La figure 2 montre comment les quantités qui nous intéressent, les probabilités d'extinction après m périodes \(x_1(m)\) et \(x_2(m)\), varient en fonction de \(s_0\). On a aussi tracé les courbes déduites de (3.4) : \[ {x}_1^*(m) = \frac{1+\frac{\delta}{\alpha(s_0) }}{1+\frac{\gamma}{\beta}}\quad ,\quad {x}^*_2(m) = \frac{1+\frac{\beta}{\gamma}}{1+\frac{\alpha(s_0)}{\delta}}\,. \] La figure 2 suggère que \(x_1(m)\) et \(x_2(m)\) convergent, lorsque \(T\to +\infty\,\), vers des limites égales à 1 si \(s_0 \in ]s^*,s_2[\) . \(s_0=s^*\) est une discontinuité des limites. Le problème est de déterminer ce point.
On démontrera dans la section suivante que les solutions \(x_1(s)\) et \(x_2(s)\) de la figure 1, qui sont très proches de 1 pour \(p:=s_0+1-s_2 < s < s_0+1-s_1\), s'écartent brusquement du voisinage de 1 pour \(s=q:=s_0+1-s^*>s_0+1-s_1\) avec \[\int_{p}^q \Lambda(s_0+m-s)\, ds =0.\] Autrement dit, ces solutions s'écartent du voisinage de 1 en un point s=q. De plus, \(q=s_0+1-s^*\) et \[\int_{s^*}^{s_2} \Lambda(s)\, ds =0.\] C'est cette équation qui détermine \(s^*\) de manière unique. En effet, si \(\phi(s)=\int_s^{s_2} \Lambda(v)\, dv\), alors on a
Pour justifier ce qui vient d'être dit au sujet du point de discontinuité, on considère plus généralement un champ lent-rapide avec deux dimensions rapides et une dimension lente, comme (3.2)-(3.3). On suppose que la dynamique rapide possède un point singulier avec deux valeurs propres réelles distinctes dont l'une est toujours négative et la deuxième est négative puis positive. Il s'agit donc d'une bifurcation transcritique où l'état d'équilibre de la dynamique rapide est un nœud stable puis un point-selle.
Une solution qui est proche du point singulier stable ne va pas quitter son voisinage dès qu'il devient instable, mais va continuer à en rester proche pendant un certain temps. Le but est de calculer la fonction entrée-sortie pour cette bifurcation transcritique, c'est-à-dire de définir l'instant où la solution s'éloigne du point singulier (instant de sortie), en fonction de celui où elle s'en est approchée (instant d'entrée). Ce phénomène connu sous le nom de « retard à la bifurcation » est lié à la notion de solutions canards et de surstabilité.
La notion de fonction entrée-sortie et le concept de solution canard ont été étudiés pour la première fois au tout début des années 1980 avec les méthodes de l'analyse non standard. Voir les articles de revue (Benoît et coll., 1981 ; Cartier, 1982 ; Zvonkin et Shubin, 1984). La fonction entrée-sortie a été calculée d'abord pour les canards de l'équation de Van der Pol (Benoît, 1981 ; Benoît et coll., 1981) puis étendue à un système lent-rapide quelconque du plan (Diener et Diener, 1983).
Plus tard, l'existence des solutions canards a été retrouvée avec les méthodes classiques des développement asymptotiques (Eckhaus, 1983) et par la théorie géométrique des perturbations singulières (Dumortier et Roussarie, 1996). La fonction entrée-sortie pour un système du plan a été obtenue aussi par la théorie géométrique des perturbations singulières (De Maesschalck et Schecter, 2016).
Pour plus de détails sur l'apport de l'école non standardiste française au problème des canards et du retard à la bifurcation, le lecteur peut consulter (Cartier, 1982 ; Fruchard et Schäfke, 2008). Pour une vue plus complète sur les divers approches dans la théorie des perturbations singulières, voir la monographie récente (Kuehn, 2015) ainsi que l'article (Wechselberger, 2007) consacré aux canards. Pour la notion de surstabilité et de retard à la bifurcation, voir aussi (Benoît, 1991, 2015 ; Benoît et coll., 1998 ; Fruchard et Schäfke, 2008 ; Wallet, 1990, 1994) et les références qu'elles contiennent.
Le cas particulier d'une champ lent-rapide en dimension deux, avec une dynamique rapide de dimension un qui est attractive puis répulsive, est bien compris, voir (Diener et Diener, 1983). Le cas de la bifurcation de Hopf, où deux valeurs propres sont complexes conjuguées et leur partie réelle change de signe, a été considéré par plusieurs auteurs, voir (Benoît, 2009 ; Callot, 1993 ; Diener et Diener, 1995 ; Lobry, 1992 ; Neishtadt, 1987, 1988 ; Wallet, 1986). Voir aussi la présentation complète et pédagogique dans la monographie récente (Kuehn, 2015, chapitre 12).
Considérons un système différentiel sur \(\mathbb{R}\times\mathbb{R}^2\) avec une variable lente \(s\in\mathbb{R}\) et avec deux variables rapides \(x\in\mathbb{R}^2\) \begin{equation} \varepsilon\frac{dx}{ds}=f(s,x). \tag{4.1} \end{equation} \(f:\mathbb{R}\times\mathbb{R}^2\rightarrow\mathbb{R}^2\) est une fonction différentiable en \((s,x)\), et \(\varepsilon>0\) est un infiniment petit. On utilise le vocabulaire de l'analyse non standard, voir (Diener et Reeb, 1989) ou Lobry (2018, chapitre 5). On suppose \(f(s,0)=0\ \forall s\).
x=0 est non seulement une courbe lente du système (4.1), c'est-à-dire une solution de l'équation \(f(s,x)=0\), mais aussi une solution particulière du système (4.1). On définit la matrice carrée 2×2 \begin{equation} M(s)=\frac{\partial f}{\partial x}(s,0). \tag{4.2} \end{equation} On suppose que \(M(s)\) possède deux valeurs propres distinctes, \(\lambda_1(s)\) et \(\lambda_2(s)\) dont l'une reste toujours négative et l'autre change de signe. Avec \(\sigma_0 < \sigma_1 < \sigma_2\), on a :
Dans la théorie géométrique des perturbations singulières on étudie le système (4.1) dans l'espace de phase étendu \((x,\varepsilon)\). On ajoute l'équation \(\frac{d\varepsilon}{ds}=0\). Une seule valeur propre de la dynamique rapide change de signe. Cette situation peut étre ramenée au cas des systèmes dans le plan, par réduction sur la variété centrale du système augmenté ((4.1), \(\frac{d\varepsilon}{ds}=0\)) en son point d'équilibre \((x,\varepsilon)=(0,0)\). Pour plus de détails voir (Boudjellaba et Sari, 2009 ; Krupa et Szmolyan, 2001). Avec cette réduction, on obtient un système plan dont la fonction entrée-sortie est donnée par l'intégrale de la valeur propre qui change de signe (Diener et Diener, 1983): \begin{equation}\tag{4.3} \int_{p}^{q}\lambda_2(s)\, ds=0\, . \end{equation} Dans cette équation p est l'instant d'entrée, et q est l'instant de sortie. La réduction prédit que la fonction entrée-sortie est donné par la formule (4.3) localement, près de la valeur de bifurcation transcritique. On se propose dans ce qui suit de calculer la fonction entrée-sortie globale. Le cas particulier d'un champ lent-rapide en dimension trois avec une dynamique rapide découplée a été considéré dans (Boudjellaba et Sari, 2009).
Nous utilisons le vocabulaire de l'analyse non standard. Ce qu'est précisément cette théorie n'est pas très important pour la compréhension de cet article. Le lecteur peut garder en tête le sens intuitif du langage infinitésimal et se rassurer en sachant que l'analyse non standard fournit une fondation rigoureuse des concepts d'infiniment petit et d'infiniment grand. Pour une introduction à l'analyse non standard, voir (Diener et Reeb, 1989). Pour plus d'informations sur l'utilisation de l'analyse non standard dans la théorie des équations différentielles, le lecteur peut se reporter à (Cartier, 1982), (Zvonkin et Shubin, 1984), (Kuehn, 2015, chapitre 19.5) ou (Lobry, 2018, chapitre 5).
On suppose donc que le paramètre ε dans (4.1) est infiniment petit. La solution \(x(s)=0\) est un « canard » puisqu'elle est attractive si \(s\in[\sigma_0,\sigma_1[\) et répulsive si \(s\in]\sigma_1,\sigma_2]\). Le but est d'étudier les solutions du système (4.1) qui sont infiniment proches de cette solution. La dynamique rapide est attractive sur l'intervalle \([\sigma_0,\sigma_1[\). On prend \(p\in[\sigma_0,\sigma_1[\,\). Une solution du système (4.1) avec une condition initiale dans le bassin d'attraction de 0 se dirige rapidement vers la courbe lente x=0 et reste infiniment proche de celle-ci tant que \(s < \sigma_1\). La solution ne quitte pas le voisinage infinitésimal de 0 à cet instant, mais continue à longer le 0 sur tout un intervalle. L'instant \(q > \sigma_1\) pour lequel \(x(s)\) n'est plus infiniment proche de 0 est appelé l'instant de sortie. L'objectif est de déterminer la fonction \(p\mapsto q\). On va montrer que q est défini par l'équation (4.3). Plus précisément on a le résultat suivant :
Preuve. On a \(g(s,x)=f(s,x)-M(s)x\). \(M(s)\) est la matrice (4.2). On a \begin{equation} g(s,0)=0,\quad \frac{\partial g}{\partial x}(s,0)=0. \tag{4.4} \end{equation} Le système (4.1) devient \begin{equation} \varepsilon\frac{dx}{ds}=M(s)x+g(s,x). \tag{4.5} \end{equation} La matrice \(M(s)\) possède deux valeurs propres distinctes. Il existe donc une matrice différentiable inversible \(P(s)\) avec \[P(s)^{-1}M(s)P(s)=A(s)\quad ,\quad A(s)=\left(\begin{array}{cc}\lambda_1(s)&0\\0&\lambda_2(s)\end{array}\right).\] On transforme l'équation (4.5) avec le changement de variable \(x=P(s)u\) \[ \varepsilon\frac{du}{ds}= A(s)u+P(s)^{-1}g(s,P(s)u)-\varepsilon P(s)^{-1}P'(s)u. \] On transforme cette équation avec la loupe \(u=\varepsilon U\) \[ \varepsilon\frac{dU}{ds}= A(s)U+\frac{1}{\varepsilon}P(s)^{-1}g(s,P(s)\varepsilon U)-\varepsilon P(s)^{-1}P'(s)U. \] Les conditions (4.4) sont vérifiées par \(g(s,x)\). On a donc \[P(s)^{-1}g(s,P(s)\varepsilon U)=\varepsilon^2 g_1(s,U,\varepsilon),\] et \(g_1(s,U,\varepsilon)\) est une fonction continue. Par conséquent, on a \[ \varepsilon\frac{dU}{ds}= A(s)U+\varepsilon h(s,U,\varepsilon). \] \(h(s,U,\varepsilon)=g_1(s,U,\varepsilon)-P(s)^{-1}P'(s)U\) est une fonction continue. On définit les composantes des vecteurs : \(U=(U_1,U_2)\) et \(h=(h_1,h_2)\). Le système devient \[ \varepsilon\frac{dU_j}{ds}=\lambda_j(s)U_j+\varepsilon\, h_j(s,U_1,U_2,\varepsilon),\qquad j=1,2. \] Ce système est constitué de deux équations faiblement couplées. Le changement de variables \[U_1=r\cos\theta,\quad U_2=r\sin\theta\] transforme le système en \begin{equation} \begin{array}{l} \varepsilon\frac{dr}{ds}=r\left [\lambda_1(s)\cos^2\theta+\lambda_2(s)\sin^2\theta\right ]+ \varepsilon \, k_1(s,r,\theta,\varepsilon),\\[2mm] \varepsilon\frac{d\theta}{ds}=\left [\lambda_2(s)-\lambda_1(s)\right]\cos\theta\sin\theta+ \varepsilon \, k_2(s,r,\theta,\varepsilon), \end{array} \end{equation} avec \begin{eqnarray*} k_1(s,r,\theta,\varepsilon)&=&\cos \theta \ h_1(s,r\cos \theta,r\sin \theta, \varepsilon) + \sin \theta\ h_2(s,r\cos \theta,r\sin \theta, \varepsilon),\\ k_2(s,r,\theta,\varepsilon)&=&-\frac{\sin \theta}{r} \, h_1(s,r\cos \theta,r\sin \theta, \varepsilon) + \frac{\cos \theta}{r}\, h_2(s,r\cos \theta,r\sin \theta, \varepsilon). \end{eqnarray*} \(k_2\) est une fonction continue en r=0 car \(h_1=O(r)\) et \(h_2=O(r)\). On choisit \(r_0\) avec \(0 < r_0 < 1\) et de sorte que la boule de centre 0 et de rayon \(r_0\) soit incluse dans le bassin d'attraction de l'origine. Appliquons le changement de variable \(v=\varepsilon\ln(r)\) à la région \( 0 < r < r_0 \), qui est envoyée dans la région définie par \(-\infty < v < \varepsilon\ln(r_0) < 0\). On obtient le système : \begin{equation}\tag{4.6} \begin{array}{l} \frac{dv}{ds}=\lambda_1(s)\cos^2\theta+\lambda_2(s)\sin^2\theta+ \varepsilon \, k_1(s,e^{v/\varepsilon},\theta,\varepsilon),\\[2mm] \varepsilon\frac{d\theta}{ds}=\left[\lambda_2(s)-\lambda_1(s)\right)]\cos\theta\sin\theta+ \varepsilon\, k_2(s,e^{v/\varepsilon},\theta,\varepsilon). \end{array} \end{equation} C'est un système singulièrement perturbé dont la variété lente est la réunion des deux plans θ=0 et θ=π/2. Parce que \(\lambda_2(s)>\lambda_1(s)\) pour tout s, le plan θ=π/2 est attractif et le plan θ=0 est répulsif. Toute solution issue d'un point non infiniment proche du plan répulsif devient infiniment proche du plan attractif en un temps infiniment petit. Les solutions qui sont issues d'un point très proche du plan répulsif peuvent rester près de ce plan un temps assez long avant de s'en éloigner. Le théorème de Tihonov s'applique (Lobry et coll., 1998 ; Tihonov, 1952). On choisit \(p\in[\sigma_0,\sigma_1[\) et \(x(p)\) une condition initiale située dans le bassin d'attraction de 0, mais qui n'est pas infiniment proche de la variété invariante de la dynamique rapide \[\frac{dx}{dt}=f(p,x)\] correspondant à la valeur propre \(\lambda_1(p)\). La dynamique rapide conduit la solution correspondante infiniment près de 0. Dans le plan \((U_1,U_2)\), elle n'est pas infiniment proche de la variété lente \(U_2=0\,\), et donc du plan θ=0. Par conséquent la solution s'approche rapidement du plan θ=π/2 puis est approximée par la solution du système lent \begin{equation} \frac{dv}{ds}=\lambda_2(s),\qquad \theta=\pi/2. \end{equation} On en déduit que \[v(s)=\int_{p}^s\lambda_2(w)\, dw.\] Par conséquent on a de nouveau \(r(s)=r_0\), c'est-à-dire \(v(s)\) infiniment petit, lorsque s est asymptotiquement égal à q défini par (4.3). Pour cette valeur de q, l'origine est un point-selle pour la dynamique rapide \[\frac{dx}{dt}=f(q,x).\] Par conséquent, la solution s'éloigne au point q du point-selle le long de sa séparatrice instable. On a utilisé ici qu'à l'instant p la solution n'était pas infiniment proche de la variété lente θ=π/2, ce qui traduit le fait que la solution n'est pas arrivée dans le plan \((U_1,U_2)\) en étant très près de \(U_1=0\). Ceci termine la preuve.
Retournons à l'exemple (3.2)-(3.3). On définit \(\tilde{\alpha}(s)=\alpha(s_0+m-s)\). Le système rapide suivant, où s est considéré comme un paramètre, \begin{equation} \begin{array}{l} \frac{dx_1}{dt}=\beta(1-x_1)-\gamma x_1(1-x_2),\\[2mm] \frac{dx_2}{dt}=\delta (1-x_2)-\tilde{\alpha}(s) (1-x_1)x_2, \end{array} \end{equation} a deux points d'équilibre (états quasi-stationnaires) \((x_1, x_2)=(1, 1)\) et \((x_1, x_2)=(x_1^*(s),x_2^*(s))\) donné par (3.4). La matrice jacobienne en (1,1) est \(\tilde{c}(s_0+m-s)\). Comme on l'a déjà vu, les deux valeurs propres sont toujours distinctes, ce sont des nombres réels. Les deux valeurs propres sont négatives si et seulement si \(\tilde{\alpha}(s) < \beta \delta /\gamma\). Par conséquent le point singulier (1,1) est un noeud attractif pour les valeurs de s pour lesquelles \(\tilde{\alpha}(s) < \beta \delta /\gamma\,\), et un point-selle si \(\tilde{\alpha}(s)>\beta \delta /\gamma\). Les valeurs propres sont \(\lambda_1(s)=\lambda_-(s)\) et \(\lambda_2(s)=\lambda_+(s)\), données par (3.5).
Avec \((x_1,x_2)=(x_1^*(s), x_2^*(s))\,\), on obtient la matrice jacobienne \[ J=\left( \begin{array}{cc} -\frac{\beta+\gamma}{1+\delta/\tilde{\alpha}(s)}&\frac{1+\delta/\tilde{\alpha}(s)}{1/\beta+1/\gamma}\\ \frac{1+\beta/\gamma}{1/\tilde{\alpha}(s)+1/\delta}&-\frac{\delta+\tilde{\alpha}(s)}{1+\beta/\gamma} \end{array} \right). \] On a \[{\rm Trace}(J) < 0\ ,\quad \quad {\rm D\acute{e}t}(J)=\tilde{\alpha}(s)\gamma-\beta \delta.\] Les valeurs propres ont une partie réelle négative si et seulement si \(\tilde{\alpha}(s)>\beta \delta /\gamma\). Par conséquent, aux points où \(\tilde{\alpha}(s)=\beta \delta /\gamma\,\), il y a des bifurcations transcritiques, car les deux équilibres suivants se rencontrent et échangent leurs stabilités : \((x_1,x_2)=(1, 1)\) et \((x_1,x_2)=(x_1^*(s), x_2^*(s))\).
On a
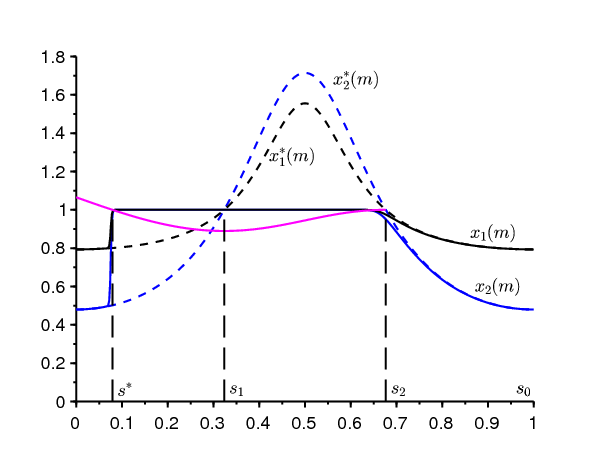
Cette étude s'étend sans doute à des problèmes avec plus de deux équations rapides et une équation lente. Considérons par exemple le système linéarisé à quatre équations rapides de (Bacaër, 2007, Section 4.2) \begin{equation} \frac{dW}{dt} = \left (\begin{array}{cccc} -(\gamma+\mu) & 0 & 0 & \psi(t/T)\\ \gamma & -\mu & 0 & 0 \\ 0 & \beta & -\delta & 0\\ 0 & 0 & \delta & -\alpha \end{array} \right )W=c(t/T) W. \end{equation} On suppose \(\alpha>0\), \(\beta>0\), \(\gamma>0\), \(\delta>0\), \(\mu>0\). \(\psi(\cdot)>0\) est une fonction périodique de période 1. C'est aussi un modèle pour la transmission d'une maladie à vecteurs. Les deux premières composantes représentent les vecteurs infectés dans la phase latente et dans la phase infectieuse tandis que les deux dernières composantes représentent les personnes infectées dans la phase latente et dans la phase infectieuse. Le système (2.1) devient, avec \(\varepsilon=1/T\) \begin{eqnarray*} \varepsilon \, \frac{dx_1}{ds}(s) &=& (\gamma+\mu) [1-x_1(s)]-\gamma [1-x_2(s)],\\ \varepsilon \, \frac{dx_2}{ds}(s) &=& \mu[1-x_2(s)]-\beta x_2(s) [1-x_3(s)],\\ \varepsilon \, \frac{dx_3}{ds}(s) &=& \delta [1-x_3(s)]-\delta [1-x_4(s)],\\ \varepsilon \, \frac{dx_4}{ds}(s) &=& \alpha [1-x_4(s)]-\psi(s_0+m-s) [1-x_1(s)] x_4(s). \end{eqnarray*} La conjecture est que la fonction entrée-sortie est donnée par la formule (4.3), où \(\lambda_2(s)\) doit être remplacé par la valeur propre réelle dominante \(\Lambda(s)\) de la matrice \(c(s)\), comme on a pu le vérifier sur un exemple numérique (Figure 3). Les valeurs des paramètres sont \(\alpha=1\), \(\beta=1\), \(\gamma=1\), \(\delta=1\), \(\mu=1\), \(\psi(s)=3\times (1+\mbox{0,75}\cos(2\pi s))\), \(m=3\) et \(T=2000\). On a l'équation caractéristique pour les valeurs propres λ de la matrice \(c(s)\) \[(\lambda+\gamma+\mu)(\lambda+\mu)(\lambda+\delta)(\lambda+\alpha)=\beta\, \gamma\, \delta\, \psi(s).\] On en déduit que \(\Lambda(s) < 0\) si et seulement si \[\frac{\beta\, \gamma\, \psi(s)}{\alpha\, \mu\, (\gamma+\mu)} < 1,\] ce qui se produit pour \(s_1 < s < s_2\) avec \(s_1\simeq \mbox{0,323}\) et \(s_2\simeq \mbox{0,677}\). Avec la formule (4.3) on trouve \(s^*\simeq \mbox{0,047}\), qui semble bien correspondre au saut brusque de la probabilité d'extinction dans la figure 3.