Sequential dimension reduction for learning features of expensive black-box functions
Résumé
Learning a feature of an expensive black-box function (optimum, contour line,...) is a difficult task when the dimension increases. A classical approach is two-stage. First, sensitivity analysis is performed to reduce the dimension of the input variables. Second, the feature is estimated by considering only the selected influential variables. This approach can be computationally expensive and may lack flexibility since dimension reduction is done once and for all. In this paper, we propose a so called Split-and-Doubt algorithm that performs sequentially both dimension reduction and feature oriented sampling. The 'split' step identifies influential variables. This selection relies on new theoretical results on Gaussian process regression. We prove that large correlation lengths of covariance functions correspond to inactive variables. Then, in the 'doubt' step, a doubt function is used to update the subset of influential variables. Numerical tests show the efficiency of the Split-and-Doubt algorithm.
Fichier principal
 main.pdf (410.29 Ko)
Télécharger le fichier
main.pdf (410.29 Ko)
Télécharger le fichier
 boxplotsperiteration.jpg (40.57 Ko)
Télécharger le fichier
boxplotsperiteration.jpg (40.57 Ko)
Télécharger le fichier
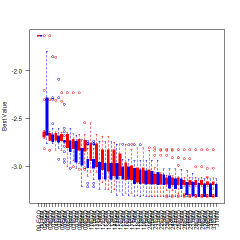 boxplotsperiteration.png (6.68 Ko)
Télécharger le fichier
Ackley20D40iterboxlot.pdf (28.03 Ko)
Télécharger le fichier
Ackley20D40itermean.pdf (21.59 Ko)
Télécharger le fichier
Borhole25Dboxlot.pdf (22.55 Ko)
Télécharger le fichier
Borhole25Dmean.pdf (19.17 Ko)
Télécharger le fichier
Branin25Dboxlot.pdf (29.21 Ko)
Télécharger le fichier
Branin25Dmean.pdf (20.59 Ko)
Télécharger le fichier
IDEAL_cos2pi_constrastxstar.pdf (51.46 Ko)
Télécharger le fichier
IDEAL_cos2pix2_1.pdf (183.23 Ko)
Télécharger le fichier
IDEAL_cos_krigx1.pdf (175.73 Ko)
Télécharger le fichier
IDEAL_loglik2.pdf (179.33 Ko)
Télécharger le fichier
IDEAL_loglik2bad.pdf (175.61 Ko)
Télécharger le fichier
IDEAL_loglikcos2pi_10_tr.pdf (178.12 Ko)
Télécharger le fichier
Rosenbrock20_5D_largerboxlot.pdf (42.8 Ko)
Télécharger le fichier
Rosenbrock20_5D_largermean.pdf (25.29 Ko)
Télécharger le fichier
harmtann15Dboxlot.pdf (26.85 Ko)
Télécharger le fichier
harmtann15Dmean.pdf (20.24 Ko)
Télécharger le fichier
hartmannbydimnewcolorcode.pdf (23.32 Ko)
Télécharger le fichier
legend.pdf (14.5 Ko)
Télécharger le fichier
meancomputingTime.pdf (18.02 Ko)
Télécharger le fichier
rosenbrock_missperc.pdf (5.7 Ko)
Télécharger le fichier
rosenperc_inf_var.pdf (5.34 Ko)
Télécharger le fichier
boxplotsperiteration.png (6.68 Ko)
Télécharger le fichier
Ackley20D40iterboxlot.pdf (28.03 Ko)
Télécharger le fichier
Ackley20D40itermean.pdf (21.59 Ko)
Télécharger le fichier
Borhole25Dboxlot.pdf (22.55 Ko)
Télécharger le fichier
Borhole25Dmean.pdf (19.17 Ko)
Télécharger le fichier
Branin25Dboxlot.pdf (29.21 Ko)
Télécharger le fichier
Branin25Dmean.pdf (20.59 Ko)
Télécharger le fichier
IDEAL_cos2pi_constrastxstar.pdf (51.46 Ko)
Télécharger le fichier
IDEAL_cos2pix2_1.pdf (183.23 Ko)
Télécharger le fichier
IDEAL_cos_krigx1.pdf (175.73 Ko)
Télécharger le fichier
IDEAL_loglik2.pdf (179.33 Ko)
Télécharger le fichier
IDEAL_loglik2bad.pdf (175.61 Ko)
Télécharger le fichier
IDEAL_loglikcos2pi_10_tr.pdf (178.12 Ko)
Télécharger le fichier
Rosenbrock20_5D_largerboxlot.pdf (42.8 Ko)
Télécharger le fichier
Rosenbrock20_5D_largermean.pdf (25.29 Ko)
Télécharger le fichier
harmtann15Dboxlot.pdf (26.85 Ko)
Télécharger le fichier
harmtann15Dmean.pdf (20.24 Ko)
Télécharger le fichier
hartmannbydimnewcolorcode.pdf (23.32 Ko)
Télécharger le fichier
legend.pdf (14.5 Ko)
Télécharger le fichier
meancomputingTime.pdf (18.02 Ko)
Télécharger le fichier
rosenbrock_missperc.pdf (5.7 Ko)
Télécharger le fichier
rosenperc_inf_var.pdf (5.34 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
| Format | Figure, Image |
|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
Loading...