\(\mathrm{Nicolas\ Baca\ddot{e}r}\)
On utilise la version min-plus de la formule du rayon spectral pour prouver que la valeur propre unique d'un problème de valeur propre min-plus dépend continûment des paramètres. On prouve aussi que la méthode numérique introduite par Chou et Griffiths pour calculer cette valeur propre converge. Une boîte à outils récemment développée par l'INRIA permet d'illustrer ces résultats. On utilise les modèles de Frenkel-Kontorova en exemple. On insiste aussi sur l'analogie avec l'homogénéisation des équations de Hamilton-Jacobi.
Mots-clés: problèmes de valeur propre min-plus; analyse numérique; modèle de Frenkel-Kontorova; équations de Hamilton-Jacobi
Certains problèmes d'optimisation peuvent se formuler en utilisant le semi-anneau \[\mathbb{R}_{\min}=(\mathbb{R}\cup \{+\infty\},\oplus,\otimes),\quad \lambda \oplus \mu=\min (\lambda,\mu)\quad \mathrm{,}\quad \lambda \otimes \mu = \lambda + \mu,\] de sorte qu'ils apparaissent comme les analogues des problèmes classiques de valeur propre. Par exemple, \[\min_{1\leq j\leq n} \{K_{i,j}+u_j\} = \lambda + u_i,\quad \quad \sum_{1\leq j\leq n} K_{i,j} \times u_j = \lambda \times u_i\] se ressemblent, ainsi que \[\min_{a\leq y\leq b} \{K(x,y)+u(y)\} = \lambda + u(x),\quad \quad \int_a^b K(x,y) \times u(y)\, dy = \lambda \times u(x).\] Ces analogies ont été utilisées pour développer sur ce semi-anneau une théorie spectrale des matrices [5] et des opérateurs intégraux [14]. [6] a utilisé une méthode numérique pour résoudre des « problèmes intégraux » de valeur propre min-plus et ainsi tracer des diagrammes de phase pour des modèles de Frenkel-Kontorova. Le principal objectif ici est de prouver la convergence de cette méthode.
La section 1, inspirée de [12], rappelle comment formaliser les analogies avec l'introduction de quelques définitions générales. La section 2 rappelle les théorèmes principaux de la théorie spectrale sur \(\,\mathbb{R}_{\min}\). La section 3 démontre que la valeur propre λ dépend continûment des paramètres qui interviennent dans la fonction K. La section 4 prouve la convergence de l'approximation numérique des problèmes de valeur propre sur \(\,\mathbb{R}_{\min}\). Les preuves des sections 3 et 4 se déduisent facilement d'une sorte de formule du rayon spectral présentée dans la section 2. La section 5 traite du cas des fonctions périodiques. La section 6 illustre les résultats précédents dans deux contextes: les modèles de Frenkel-Kontorova en physique du solide et l'homogénéisation des équations de Hamilton-Jacobi.
Mentionnons que les problèmes de valeur propre à paramètre pour les équations de Hamilton-Jacobi, qui sont équivalents à des problèmes de valeur propre min-plus, apparaissent aussi dans l'étude des ondes progressives pour la propulsion à propergol solide [3,15]. Cette application était la motiviation initiale pour notre étude. Mais comme les détails techniques sont plus compliqués, on les expliquera ailleurs.
Notons aussi que l'analyse numérique d'autres problèmes linéaires min-plus n'est pas toujours aussi simple que celle des problèmes de valeur propre présentée ici (voir [4] pour une discussion).
Définition. \(\mathcal{R}\) est un ensemble muni d'une loi de composition interne \(+\). \((\mathcal{R},+)\,\) est un semi-groupe si + est associatif et a un élément neutre. \((\mathcal{R},+)\) est un semi-groupe commutatif si + est aussi commutatif.
Définition. \(\mathcal{R}\) est un ensemble muni de deux lois de composition interne + et ×. \((\mathcal{R},+,\times)\,\) est un semi-anneau si
Exemples.
Définition. \((\mathcal{R},+,\times)\) est un semi-anneau et \((X,+)\,\) un semi-groupe commutatif. On suppose que \(\forall \lambda \in \mathcal{R},\ \forall x\in X\), \(\lambda \cdot x\in X\). On dit que \(\,(X,+,\cdot)\,\) est un semi-module sur \(\,(\mathcal{R},+,\times)\) si \(\forall \lambda,\mu \in \mathcal{R}\), \(\forall x,y \in X\), \begin{align*} &(\lambda+\mu) \cdot x=\lambda \cdot x + \mu \cdot x\, ,\\ & (\lambda \times \mu) \cdot x = \lambda \cdot (\mu \cdot x),\\ &\lambda \cdot (x+y)=\lambda \cdot x + \lambda \cdot y,\\ & 1\cdot x=x. \end{align*} On dit que Y est un sous-semi-module de X si Y est un semi-module et \(\,Y \subset X\).
Exemple. Soit X un ensemble et \(\,(\mathcal{R},+,\times)\,\) un semi-anneau. \[\forall f,g \in \mathcal{R}^X,\quad \forall x\in X, \quad (f+g)(x):=f(x)+g(x),\quad (\lambda\cdot f)(x):=\lambda \times f(x).\] \((\mathcal{R}^X,+,\cdot)\) est alors un semi-module sur \(\mathcal{R}\).
Exemple. Soit X un ensemble et \(\,B(X,\mathbb{R}_{\min})\) l'ensemble des fonctions \(X \to \mathbb{R}_{\min}\,\) qui sont bornées inférieurement. \(B(X,\mathbb{R}_{\min})\) est un sous-semi-module de \((\mathbb{R}_{\min}^X,\min,+)\).
Définition. \((\mathcal{R},+,\times)\) est un semi-anneau. \((X,+,\cdot)\) et \((Y,+,\cdot)\) sont deux semi-modules et \(L:X\to Y\). On dit que L est un opérateur linéaire si \(\,\forall \lambda,\mu \in \mathcal{R}\), \(\forall x,y \in X\), \(L(\lambda\cdot x + \mu \cdot y)=\lambda \cdot L(x) + \mu \cdot L(y)\).
Exemple. Soit X un ensemble et \(\,K:X^2\to \mathbb{R}_{\min}\) une fonction bornée inférieurement. \(\mathcal{K}\) est l'application de \(B(X,\mathbb{R}_{\min})\) dans lui-même \(u \mapsto \mathcal{K}u\) avec \[\forall x \in X,\quad (\mathcal{K}u)(x)=\inf_{y\in X} \{K(x,y)+u(y) \}.\] \(\mathcal{K}\) est un opérateur linéaire.
Définition. \((\mathcal{R},+,\times)\) est un semi-anneau, \((X,+,\cdot)\) un semi-module sur \(\mathcal{R}\), \(L:X\to X\) un opérateur linéaire et \(\lambda \in \mathbb{R}\). On dit que λ est une valeur propre de L si \(\exists x\in X,\ x \neq 0,\ L(x)=\lambda\cdot x\). Dans ce cas, on dit que x est un vecteur propre associé à λ.
Exemple. Mêmes notations que l'exemple précédent. \(\,\lambda \in \mathbb{R}_{\min}\) est une valeur propre de \(\mathcal{K}\) s'il existe \(u\in B(X,\mathbb{R}_{\min})\,\) avec u non identiquement +∞ et \begin{equation}\tag{1} \forall x \in X,\quad \inf_{y\in X} \{K(x,y)+u(y) \}=\lambda + u(x). \end{equation}
Théorème 1. Soit X un ensemble et \(\,K:X^2\to \mathbb{R}\,\) une fonction qui est bornée inférieurement. Supposons qu'il existe \(\,\lambda \in \mathbb{R}\) et une fonction bornée inférieurement \(u:X\to \mathbb{R}\) avec (1). On a alors \begin{equation}\tag{2} \lambda = \inf_{(x_n) \in X^{\mathbb{N}}} \liminf_{n \to +\infty} \frac{K(x_0,x_1)+\cdots+K(x_{n-1},x_n)}{n}\, . \end{equation}
Cette formule est l'analogue pour \(\mathbb{R}_{\min}\,\) de la formule du rayon spectral. [6] la donne sans précision pour \(\,X=[0,1]\). [16] ne la donne que pour un ensemble X qui est fini. Dans ce cas, la formule (3) ci-dessous est plus intéressante. Pour une interprétation de la formule en terme de rayon spectral dans une semi-algèbre normée, voir [3].
Preuve. On choisit \(\,(x_n) \in X^{\mathbb{N}}\). On a alors \[\forall n \in \mathbb{N}^*,\quad \lambda+u(x_{n-1}) = \inf_{y \in X} \{K(x_{n-1},y)+u(y) \} \leq K(x_{n-1},x_n)+u(x_n).\] Additionnons les n premières équations. On obtient \[\forall n\in \mathbb{N}^*,\quad n\lambda + u(x_0) \leq K(x_0,x_1)+\cdot + K(x_{n-1},x_n)+u(x_n).\] Puisque u est borné, divisons par n et prenons \(\,n \to +\infty\). On obtient \[\lambda \leq \liminf_{n \to +\infty} \frac{K(x_0,x_1)+\cdots+K(x_{n-1},x_n)}{n}\, .\] \((x_n)\,\) était arbitraire. On a donc \[\lambda \leq \inf_{(x_n) \in X^{\mathbb{N}}} \liminf_{n \to +\infty} \frac{K(x_0,x_1)+\cdots+K(x_{n-1},x_n)}{n}\, .\] Pour prouver l'inégalité opposée, soit ε>0 et \(y_0 \in X\). On peut construire par récurrence une suite \(\,(y_n) \in X^{\mathbb{N}}\) avec \[\forall n \in \mathbb{N}^*,\quad K(y_{n-1},y_n)+u(y_n) \leq \inf_{x \in X} \{K(y_{n-1},x)+u(x)\} + \varepsilon = \lambda +u(y_{n-1})+\varepsilon.\] Additionnons les n premières équations et divisons par n. On obtient \[\forall n \in \mathbb{N}^*,\quad \frac{K(y_0,y_1)+\cdots+K(y_{n-1},y_n)}{n} + \frac{u(y_n)}{n} \leq \lambda + \frac{u(y_0)}{n} + \varepsilon.\] Avec \(n\to +\infty\,\), on obtient \begin{align*} \lambda &\geq \liminf_{n\to +\infty} \frac{K(y_0,y_1)+\cdots+K(y_{n-1},y_n)}{n}-\varepsilon \\ &\geq \inf_{(x_n) \in X^{\mathbb{N}}} \liminf_{n \to +\infty} \frac{K(x_0,x_1)+\cdots+K(x_{n-1},x_n)}{n}-\varepsilon. \end{align*}
Théorème 2. Soit un espace métrique compact \(\,(X,d)\) et \(K\in C^0(X^2,\mathbb{R})\). Il existe un unique \(\,\lambda \in \mathbb{R}\) pour lequel il existe \(u \in C^0(X,\mathbb{R})\) avec (1).
C'est un analogue pour \(\mathbb{R}_{\min}\,\) du théorème de \(\text{Krein}\,\) et Rutman. [5] donne une preuve pour un ensemble X qui est fini. [7] donne une preuve pour \(\,X=[0,1]\,\) et note que diverses généralisations sont possibles. [9] étend la preuve à \(\,X=[0,1]^n\). [14] donne une preuve dans le cadre général et même avec des hypothèses plus faibles. Mais la méthode de preuve de [14] est un peu différente de celle utilisée dans [7,9] et moins claire. La preuve ci-dessous est une généralisation directe de celle dans [7,9].
Preuve. \(E=C^0(X,\mathbb{R})\). On définit \(\,\|u\|=\sup_{x\in X} |u(x)|\) si \(u \in E\). Alors E est un espace de Banach. On définit \[\forall u \in E,\quad \forall x\in X,\quad (Tu)(x)=\inf_{y \in X} \{K(x,y)+u(y)\}-\inf_{z\in X} \inf_{y \in X} \{K(z,y)+u(y)\}.\] \(T(E)\,\) est un ensemble équicontinu. En effet, soit ε>0. Puisque K est uniformément continu, \[\exists \alpha > 0, \quad \forall x,y,x',y' \in X,\quad \max \{d(x,x');d(y,y')\} \leq \alpha \ \Rightarrow \ |K(x,y)-K(x',y')| \leq \varepsilon.\] On choisit \(\,x,x' \in X\) avec \(d(x,x') \leq \alpha\). On a alors \begin{align*} \forall u \in E,\quad (Tu)(x)-(Tu)(x')&= \inf_{y \in X} \{K(x,y)+u(y)\} - \inf_{y \in X} \{K(x',y)+u(y)\}\\ &\leq \inf_{y \in X} \{K(x',y)+\varepsilon+u(y)\}-\inf_{y \in X} \{K(x',y)+u(y)\}=\varepsilon. \end{align*} Avec \(x'\,\) à la place de x, on obtient \(\,|(Tu)(x)-(Tu)(x')| \leq \varepsilon\).
La fonction \(T:E\to E\), \(u\mapsto Tu\ \) est continue. Avec \(\,u,v \in E\), \begin{align*} \forall x\in X,\quad (Tv)(x) &= \inf_{y \in X} \{K(x,y)+v(y)-u(y)+u(y)\} \\ &\quad \quad - \inf_{z \in X} \inf_{y \in X} \{K(z,y)+v(y)-u(y)+u(y)\}\\ &\leq (Tu)(x)+\sup_{y \in X} \{v(y)-u(y)\} - \inf_{y \in X} \{v(y)-u(y)\}\\ &\leq (Tu)(x) + 2 \|v-u\|. \end{align*} Échangeons les rôles de v et u. On obtient \(\,\|Tv-Tu\| \leq 2 \|v-u\|\).
On définit \[K_-=\inf_{x,y\in X} K(x,y),\quad K_+=\sup_{x,y\in X} K(x,y),\] \[C=\{u \in E;\ \forall x\in X,\ 0 \leq u(x) \leq K_+-K_-\}.\] On a \[\forall u \in E, \quad \forall x\in X,\quad 0 \leq (Tu)(x) \leq \inf_{y \in X} \{K_++u(y)\} - \inf_{z \in X} \inf_{y \in X} \{K_-+u(y)\} = K_+-K_-.\] On a donc \(T(E) \subset C\). En particulier, \(\,T(C) \subset C\) et \(T(C)\,\) est borné. \(\,T(E)\) est équicontinu. \(T(C)\,\) est donc aussi équicontinu. \(\,T(C)\) est relativement compact dans E d'après le théorème d'Ascoli et Arzela. \(C\,\) est un sous-ensemble fermé et convexe. Pour une fonction continue d'un sous-ensemble fermé et convexe d'un espace de Banach à valeurs dans un sous-ensemble compact de C, il y a un point fixe d'après le théorème de Schauder : \(\exists u \in C,\ Tu=u\), ce qui signifie (1) avec \[\lambda= \inf_{z\in X} \inf_{y \in X} \{K(z,y)+u(y)\}.\] L'unicité de la valeur propre λ résulte du théorème 1.
Les problèmes de valeur propre min-plus qui dépendent d'un paramètre ne semblent pas avoir été encore étudiés.
Proposition 1. Soit un espace métrique compact \(\,(X,d)\), Ω un espace topologique et \(K:\alpha \mapsto K_\alpha\) une fonction continue de \(\Omega \to (C^0(X^2,\mathbb{R}),\|\cdot\|_\infty)\). \(\,\lambda_\alpha\) est l'unique nombre réel associé à \(K_\alpha\) d'après le théorème 2. On a alors : \(\alpha \mapsto \lambda_\alpha\) de \(\Omega\to \mathbb{R}\) est une fonction continue.
Preuve. On choisit \(\,\alpha \in \Omega\) et \(\varepsilon > 0\). Il existe un voisinage \(\,\mathcal{V}\) de \(\alpha\) avec \[\beta \in \mathcal{V} \Rightarrow \sup_{x,y \in X} |K_\alpha(x,y)-K_\beta(x,y)|\leq \varepsilon.\] On a alors \begin{align*} \forall (x_n) \in X^{\mathbb{N}}, \quad \forall n \in \mathbb{N}^*,\quad \frac{K_\alpha(x_0,x_1)+\cdots+K_\alpha(x_{n-1},x_n)}{n} - \varepsilon &\leq \frac{K_\beta(x_0,x_1)+\cdots+K_\beta(x_{n-1},x_n)}{n}\\ &\leq \frac{K_\alpha(x_0,x_1)+\cdots+K_\alpha(x_{n-1},x_n)}{n}+\varepsilon. \end{align*} Prenons d'abord la \(\liminf_{n\to +\infty}\) de ces inégalités, puis l'infimum sur tous les \((x_n) \in X^{\mathbb{N}}\). On obtient, d'après la formule (2), que \[\lambda_\alpha - \varepsilon \leq \lambda_\beta \leq \lambda_\alpha+\varepsilon.\]
Proposition 2. Soit un espace métrique compact \(\,(X,d)\) et Ω un sous-ensemble convexe d'un espace vectoriel réel. \(K_\alpha \in C^0(X^2,\mathbb{R})\) si \(\,\alpha \in \Omega\). On suppose \(\, \forall x,y \in X\), \(\alpha \mapsto K_\alpha(x,y)\) de \(\Omega\to \mathbb{R}\) est une fonction concave. \(\lambda_\alpha\) est l'unique nombre réel associé à \(K_\alpha\) par le théorème 2. On a alors : \(\alpha \mapsto \lambda_\alpha\) de \(\Omega\to \mathbb{R}\) est une fonction concave.
[6] mentionne cette propriété pour \(X=[0,1]\) et \(\Omega=\mathbb{R}\).
Preuve. Avec \(\,{\bf x}=(x_n) \in X^{\mathbb{N}}\), \(n \in \mathbb{N}^*\) et \(\alpha \in \Omega\), on définit \[S(\mathbf{x},n,\alpha)=\frac{K_\alpha(x_0,x_1)+\cdots+K_\alpha(x_{n-1},x_n)}{n}\, .\] On choisit \(t \in ]0,1[\) et \(\alpha,\beta \in \Omega\). On a alors \[\forall \mathbf{x} \in X^{\mathbb{N}}, \quad \forall n \in \mathbb{N}^*,\quad S(\mathbf{x},n,t\cdot \alpha+(1-t)\cdot \beta) \geq t\, S(\mathbf{x},n,\alpha)+(1-t) S(\mathbf{x},n,\beta)\] à cause de l'hypothèse de concavité. Avec les propriétés de \(\,\liminf\), on obtient \[ \forall x\in X^{\mathbb{N}},\quad \liminf_{n \to +\infty} S(\mathbf{x},n,t\cdot \alpha + (1-t) \cdot \beta) \geq t\ \liminf_{n \to +\infty} S(\mathbf{x},n,\alpha) + (1-t)\ \liminf_{n \to +\infty} S(\mathbf{x},n,\beta).\] Prenons l'infimum sur tous les \(\mathbf{x} \in X^{\mathbb{N}}\), on obtient \begin{align*} &\inf_{\mathbf{x} \in X^{\mathbb{N}}}\liminf_{n \to +\infty} S(\mathbf{x},n,t\cdot \alpha + (1-t) \cdot \beta) \\ &\quad \quad \geq t \inf_{\mathbf{x} \in X^{\mathbb{N}}} \liminf_{n \to +\infty} S(\mathbf{x},n,\alpha) + (1-t) \inf_{\mathbf{x} \in X^{\mathbb{N}}} \liminf_{n \to +\infty} S(\mathbf{x},n,\beta). \end{align*} Donc d'après la formule (2), \(\lambda_{t\cdot \alpha + (1-t) \cdot \beta} \geq t\, \lambda_\alpha + (1-t) \lambda_\beta\).
La proposition suivante prouve la convergence de la méthode numérique utilisée par [6].
Proposition 3. Soit un espace métrique compact \(\,(X,d)\). Soit une fonction lipschitzienne \(\,K:X^2 \to \mathbb{R}\) \[\exists \kappa > 0,\quad \forall x,x',y,y' \in X,\quad |K(x,y)-K(x',y')|\leq \kappa \max \{d(x,x');d(y,y')\}.\] D'après le théorème 2, soit λ l'unique nombre réel pour lequel \(\exists\ u\in C^0(X,\mathbb{R})\,\) avec (1). Soit une suite de sous-ensembles finis de X, \((X_p)_{p\in \mathbb{N}}\,\), avec \[h_p=\sup_{x \in X} \min_{y \in X_p} d(x,y) \mathop{\longrightarrow}_{p \to +\infty} 0.\] D'après le théorème 2, \[\forall p\in \mathbb{N},\quad \exists ! \, \lambda_p\in \mathbb{R},\quad \exists \, u_p: X_p \to \mathbb{R},\quad \forall x\in X_p,\quad \min_{y \in X_p} \{K(x,y)+u_p(y)\} = \lambda_p +u_p(x).\] On a alors \(\lambda \leq \lambda_p \leq \lambda + \kappa\, h_p\) et \(\lambda_p \to \lambda\) si \(p\to +\infty\).
Cette proposition est liée au point de vue de l'analyse non-standard de [10], qui considère des valeurs de p infiniment grandes.
Preuve. On choisit \(\,p \in \mathbb{N}\). D'après (2), \begin{align*} \lambda &= \inf_{(x_n) \in X^{\mathbb{N}}} \liminf_{n \to +\infty} \frac{K(x_0,x_1)+\cdots+K(x_{n-1},x_n)}{n}\, ,\\ \lambda_p &= \inf_{(x_n) \in X_p^{\mathbb{N}}} \liminf_{n \to +\infty} \frac{K(x_0,x_1)+\cdots+K(x_{n-1},x_n)}{n}\, . \end{align*} D'un côté, \(X_p \subset X\), on a donc \(\lambda \leq \lambda_p\). D'un autre côté, soit ε>0. Il existe \(\,(x_n)\in X^{\mathbb{N}}\,\) avec \[\lambda \leq \liminf_{n \to +\infty} \frac{K(x_0,x_1)+\cdots+K(x_{n-1},x_n)}{n} \leq \lambda + \varepsilon\, .\] Par hypothèse, \(\forall n \in \mathbb{N}\), \(\exists y_n \in X_p\), \(d(x_n,y_n)\leq h_p\). Mais K est lipschitzienne, donc \(\,\forall n \in \mathbb{N}\), \(|K(x_n,x_{n+1})-K(y_n,y_{n+1})| \leq \kappa\, h_p\). En conclusion, \begin{align*} \lambda_p &\leq \liminf_{n \to +\infty} \frac{K(y_0,y_1)+\cdots+K(y_{n-1},y_n)}{n}\\ &\leq \liminf_{n \to +\infty} \frac{K(x_0,x_1)+\cdots+K(x_{n-1},x_n)}{n} + \kappa\, h_p \leq \lambda + \varepsilon + \kappa \, h_p. \end{align*} Parce que ε était arbitraire, on obtient \(\lambda_p \leq \lambda + \kappa\, h_p\).
Proposition 4. Soit un ensemble avec q éléments, \(\,X_p\). On a alors \begin{equation}\tag{3} \lambda_p = \min_{1\leq n\leq q}\ \min_{(x_0,\ldots,x_{n-1}) \in X_p^n} \frac{K(x_0,x_1)+\cdots+K(x_{n-1},x_n)}{n}\, . \end{equation}
Preuve. Voir [5] par exemple.
\(\lambda_p\,\) est la « moyenne cyclique minimale ». Cette moyenne se calcule avec un nombre fini d'opérations. La preuve est semblable à celle de (2). Néanmoins, ce n'est pas la formule (3) que l'on utilise en pratique. Il y a de meilleurs algorithmes, comme l'algorithme de Karp qui nécessite \(\,O(q^3)\,\) opérations, ou l'algorithme de Howard qui semble être le plus rapide [8]. Noter que dans l'analyse numérique des problèmes de valeur propre min-plus, les matrices impliquées sont pleines et très grandes. Donc les algorithmes efficaces sont bienvenus, en particulier lorsqu'en plus le problème dépend d'un paramètre que l'on varie comme dans les prochaines sections. L'algorithme de Karp est très facile à programmer, tandis que celui de Howard est disponible à travers la boîte à outils Maxplus de Scilab. Voir www-rocq.inria.fr/scilab/ et www-rocq.inria.fr/scilab/contributions.html.
Proposition 5. Soit un groupe topologique abélien \(\,(X,+)\), une fonction bornée inférieurement \(K:X^2 \to \mathbb{R}\,\) et P un sous-groupe de X. On suppose
\[\forall p \in P,\ \forall (x,y) \in X^2,\ K(x+p,y+p)=K(x,y).\]
\((\mathbf{X},+)\,\) est le groupe topologique qui est le quotient de X par P. On définit
\begin{equation}\tag{4}
\forall \mathbf{x},\mathbf{y} \in \mathbf{X},\quad \mathbf{K}(\mathbf{x},\mathbf{y})=\inf_{y \in \mathbf{y}} K(x,y)
\end{equation}
avec \(x \in \mathbf{x}\). Soit λ \(\in \mathbb{R}\).
[6] prouve cette proposition pour \(X=\mathbb{R}\) et \(P=\mathbb{Z}\), [9] pour \(X=\mathbb{R}^n\) et \(P=\mathbb{Z}^n\).
Preuve. Notons d'abord que \(\,\mathbf{K}\) est bien défini, parce que \[\forall x\in X, \quad \forall \mathbf{y} \in \mathbf{X}, \quad \forall p \in P,\quad \inf_{y \in \mathbf{y}} K(x+p,y) = \inf_{y \in \mathbf{y}} K(x,y-p)=\inf_{y \in \mathbf{y}} K(x,y).\] Le reste se déduit facilement du fait que si \(\mathbf{x} \in \mathbf{X}\) et \(x \in \mathbf{x}\), on a \begin{align*} \inf_{y \in X} \{K(x,y)+u(y)\}=\inf_{\mathbf{y} \in \mathbf{X}} \inf_{y \in \mathbf{y}} \{K(x,y)+u(y)\} &=\inf_{\mathbf{y} \in \mathbf{X}} \inf_{y \in \mathbf{y}} \{K(x,y)+\mathbf{u}(\mathbf{y})\}\\ &= \inf_{\mathbf{y} \in \mathbf{X}} \{\mathbf{K}(\mathbf{x},\mathbf{y})+\mathbf{u}(\mathbf{y})\}. \end{align*}
Pour tout α \(\in \mathbb{R}\,\), \(K_\alpha \in C^0(\mathbb{R}^2,\mathbb{R})\). On suppose que \begin{align} \forall x,y \in \mathbb{R}, \forall \alpha \in \mathbb{R},\quad K_0(x+1,y+1)&=K_0(x,y)\tag{7}\\ K_\alpha(x,y)&=K_0(x,y)-\alpha(x-y).\tag{8} \end{align} On définit \begin{equation} \forall \alpha \in \mathbb{R}, \quad \lambda_\alpha=\inf_{(x_n) \in \mathbb{R}^{\mathbb{N}}} \liminf_{n \to +\infty} \frac{K_\alpha(x_0,x_1)+\cdots+K_\alpha(x_{n-1},x_n)}{n}\, . \end{equation} \(\mathbb{R}/\mathbb{Z}\,\) est compact. D'après le théorème 2 et la proposition 5, \(\lambda_\alpha\) est l'unique nombre réel pour lequel il existe une fonction périodique de période 1, \(\,u_\alpha \in C^0(\mathbb{R},\mathbb{R})\,\) avec \begin{equation}\tag{9} \forall x \in \mathbb{R},\quad \inf_{y \in \mathbb{R}} \{K_\alpha(x,y)+u_\alpha(y) \} = \lambda_\alpha +u_\alpha(x). \end{equation} D'après la proposition 2, \(\alpha \mapsto \lambda_\alpha\) est une fonction concave. Donc elle a une dérivée du côté droit \(\,\frac{d\lambda}{d\alpha}(\alpha^+)\) pour tout α, et \(\alpha \mapsto \frac{d\lambda}{d\alpha}(\alpha^+)\) est une fonction décroissante.
On choisit \(L\in C^0(\mathbb{R}^2,\mathbb{R})\). On suppose
\[\forall x,y \in \mathbb{R},\quad L(x+1,y+1)=L(x,y).\]
On définit
\[\forall \alpha \in \mathbb{R}, \quad \forall x,y \in \mathbb{R},\quad K_\alpha(x,y)=L(x,y)-\alpha(x-y).\]
Les hypothèses (7) et (8) sont vérifiées. Un cas particulier est celui où \(\,V \in C^0(\mathbb{R},\mathbb{R})\) est périodique de période 1 et
\[ \forall x,y \in \mathbb{R},\quad L(x,y)=V(x)+\frac{(y-x)^2}{2}\, .\]
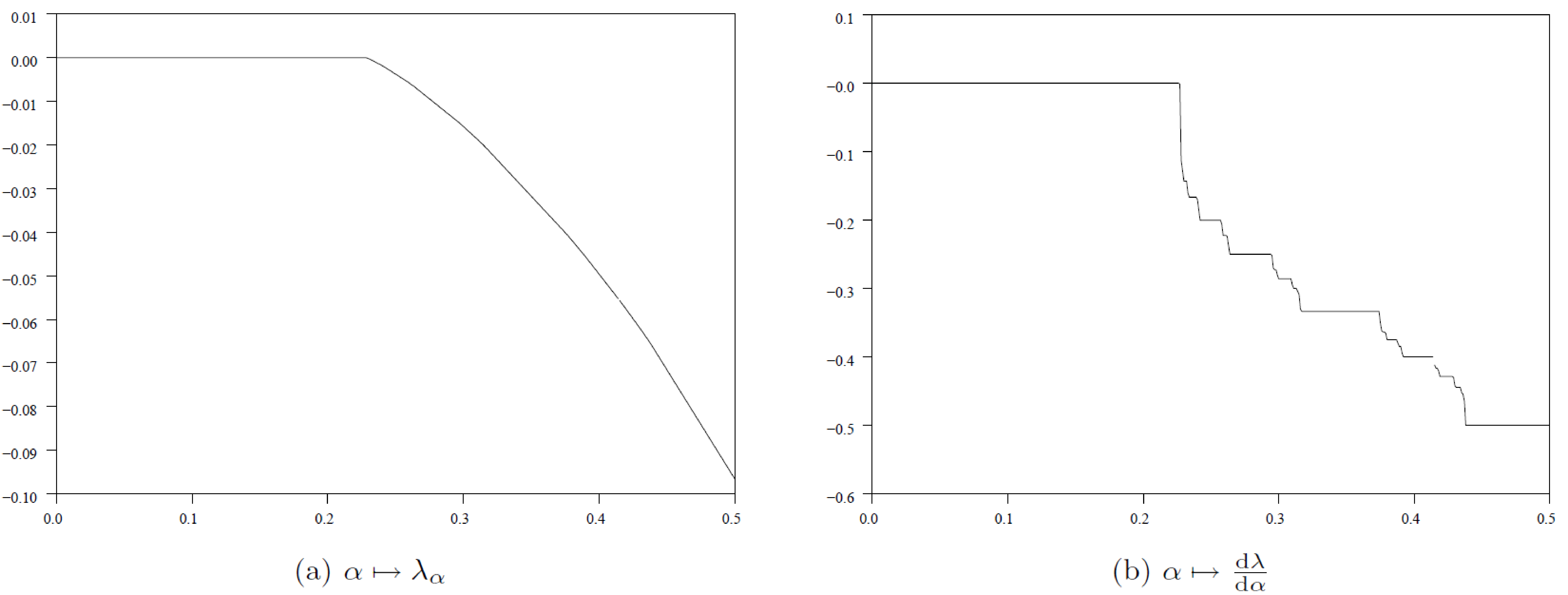
La figure 1 montre la dépendance de \(\lambda_\alpha\) par rapport à α si \(V(x)=C[1-\cos(2\pi x)]\) avec un autre paramètre \(\,C\,\). Frenkel et Kontorova ont proposé cet exemple en 1938. On prend \(\,C=(4/3)/(2\pi)^2\). On prend \(\,\{0,1/p,2/p,\ldots,(p-1)/p\}\) pour discrétiser \(\mathbb{R}/\mathbb{Z}\). On a
\[\forall \alpha \in [0,1/2],\quad \forall x,y \in [0,1],\quad \inf_{p \in \mathbb{Z}} K_\alpha(x,y+p)=V(x) + \inf_{p\in \{-1,0,1\}} \left \{ \frac{(y-x+p)^2}{2}-\alpha (x-y-p) \right \}.\]
La figure (a) illustre la continuité de \(\alpha \mapsto \lambda_\alpha\). La figure (b) suggère que \(\,\frac{d\lambda}{d\alpha}(\alpha^+)\,\) est aussi une fonction continue de α, mais comme un « escalier du diable ». Un doute subsiste pour savoir si ceci peut se déduire des résultats d'Aubry [1,2] et des remarques de Griffith [13].

On choisit \(\,L \in C^0(\mathbb{R}^2,\mathbb{R})\). On suppose
\[\forall x,v \in \mathbb{R}, \quad L(x+1,v)=L(x,v).\]
On définit
\begin{align}
\forall \alpha \in \mathbb{R},\quad \forall x,y \in \mathbb{R},\quad K_0(x,y)&=\inf \left \{ \int_0^1 L(\xi(s),\dot{\xi}(s))\, ds\, ;\ \xi \in C^1([0,1],\mathbb{R}),\ \xi(0)=y, \, \xi(1)=x \right \}, \nonumber\\
K_\alpha(x,y)&=K_0(x,y)- \alpha (x-y) \tag{10}
\end{align}
Les hypothèses (7) et (8) sont vérifiées. Un cas particulier de cette situation est celui où \(\,V \in C^0(\mathbb{R},\mathbb{R})\) est périodique de période 1, et
\[\forall x,v \in \mathbb{R},\quad L(x,v)=V(x)+\frac{v^2}{2}\, .\]
Dans cette situation, il y a une formule presque explicite pour la valeur propre \(\lambda_\alpha\) (voir [9] par exemple), à savoir
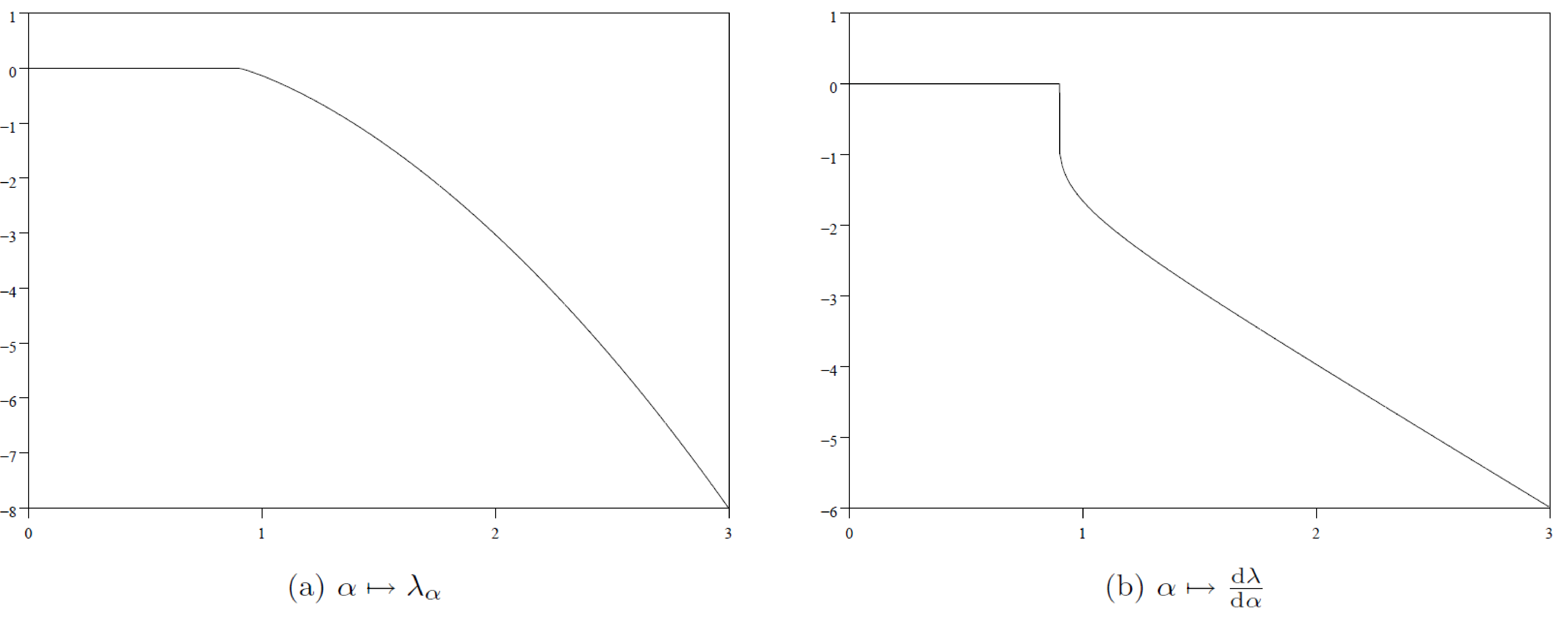
\[\lambda_\alpha = \left \{ \begin{array}{ll}
\min V & \forall\ |\alpha| \leq \int_0^1 \sqrt{2[V(x)-\min V]}\, dx\\
\lambda,\quad |\alpha|=\int_0^1 \sqrt{2[V(x)-\lambda]}\, dx & \forall\ |\alpha| > \int_0^1 \sqrt{2[V(x)-\min V]}\, dx.
\end{array}\right.\]
La figure 2 montre la dépendance de \(\lambda_\alpha\) par rapport à α si \(\,V(x)=1-\cos(2\pi x)\). Notez les similitudes et les différences avec la figure 1. Il est étrange que deux modèles aussi proches aient des comportements si différents.
Dans le cas où \(L(x,v)\,\) est convexe par rapport à v, [9] montre que le problème de valeur propre (9) avec la fonction (10) est équivalent au problème pour une cellule \[H\left (x,\alpha+\frac{\partial u}{\partial x}(x) \right )=\bar{H}(\alpha),\] avec \(\bar{H}(\alpha)=-\lambda_\alpha\) et \[\forall x,p \in \mathbb{R},\quad H(x,p)=\sup_{v \in \mathbb{R}} \left \{p\cdot v - L(x,v) \right \}.\] Rappelons que ce problème pour une cellule vient de l'homogénéisation quand \(\varepsilon \to 0\) de l'équation \[\frac{\partial v}{\partial t}(t,x)+H\left ( \frac{x}{\varepsilon},\frac{\partial v}{\partial x}(t,x) \right )=0.\] [11] expose d'autres liens entre la théorie d'Aubry et Mather et les équations de Hamilton et Jacobi. Notez aussi que la méthode numérique, qui est assez facile pour le modèle de Frenkel et Kontorova, n'est pas facile à adapter au cas des équations de Hamilton et Jacobi car le noyau (10) est déjà difficile à calculer. Dans certains cas, on pourrait utiliser un logiciel qui résout les problèmes aux limites liés à l'équation d'Euler et Lagrange pour (10). Ceci nécessite d'être étudié par ailleurs.
Retournons aux modèles de Frenkel et Kontorova. Comme dans [6], on choisit la fonction périodique de périod 1, parabolique par morceaux, \(\,V:\mathbb{R} \to \mathbb{R}\), avec
\[V(x)=\left \{ \begin{array}{ll}
\frac{c}{2}\, x^2 & \ -1/4 \leq x \leq 1/4,\\
\frac{c}{16}-\frac{c}{2} \left (x-\frac{1}{2} \right )^2 & \ 1/4 \leq x \leq 3/4
\end{array}\right.\]
avec \(c\geq 0\). On utilise \(\,\{0,1/p,2/p,\ldots,(p-1)/p \}\,\) pour la discrétisation. D'après la proposition 3 avec \(\,h_p=1/p\,\), on a
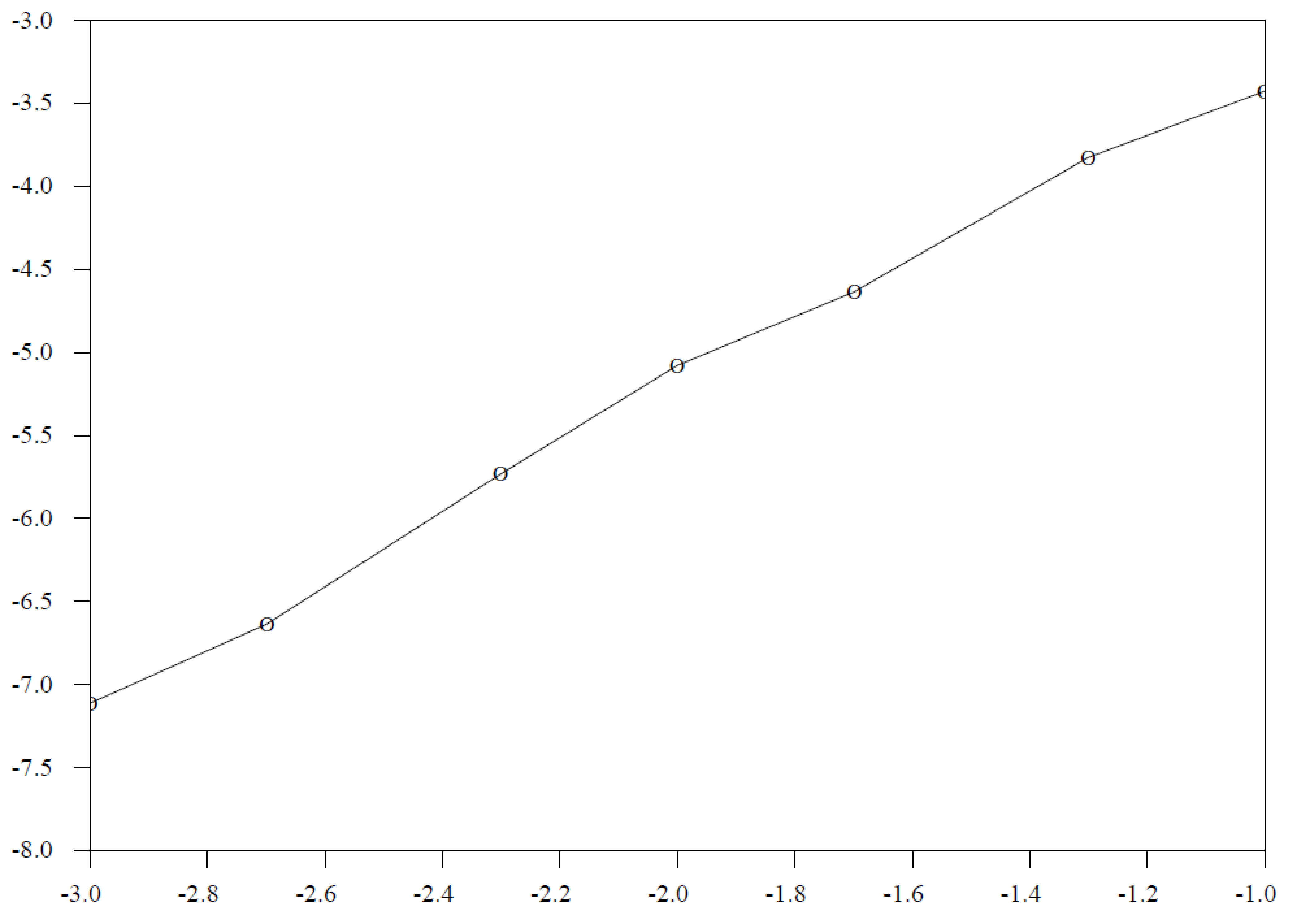
\[\log_{10}(\lambda_p-\lambda) \leq \log_{10} (\kappa) - \log_{10}(p).\]
κ est la constante de lipschitz de la fonction \(\mathbf{K}\,\) définie par (4). On suppose \(\,c=4/3\) et \(\alpha=13/32\). Alors λ se calcule explicitement, comme indiqué dans [6], à savoir \(\,\lambda=-\frac{265}{2048}\). La figure 3 montre \(\,\log_{10}(\lambda_p-\lambda)\) en fonction de \(-\log_{10}(p)\). À cause de propriétés spécifiques de K, la pente de la fonction semble proche de 2, ce qui suggère que l'erreur est quadratique. Cependant, on peut construire des exemples de problèmes de valeur propre min-plus pour lesquels la vitesse de convergence n'est que linéaire. Il reste à trouver des hypothèses suffisantes sur le noyau pour que la convergence soit quadratique.
L'auteur remercie Lin Yi-Jiun et l'Université de Colombie britannique pour l'atelier stimulant sur les méthodes de viscosité pour les équations aux dérivées partielles.