
\(\mathrm{Institut\ de\ Recherche\ pour\ le\ D\acute{e}veloppement}\), Bondy, France
Université Pierre et Marie Curie, Les Cordeliers, Paris, France
nicolas.bacaer@ird.fr
Dans un environnement aléatoire qui est une chaîne de Markov en temps continu à deux états, le temps moyen jusqu'à extinction du modèle stochastique SIS pour une épidémie croît, dans le cas surcritique, exponentiellement par rapport à la taille de la population si les deux états sont favorables, et suivant une loi de puissance si l'un des états est favorable alors que l'autre est défavorable à la propagation.
Soit N la taille de la population, supposée constante. Dans le modèle stochastique SIS pour une épidémie, chaque individu est soit sain (S), soit infecté (I) (Nåsell, 2011). Imaginons que l'environnement suive une chaîne de Markov en temps continu à deux états. \(q_j\) (\(j=1,2\)) est le taux de sortie de l'état j. Dans l'environnement j, le taux de contact de chaque individu est \(\,a_j > 0\). Si à un instant t le nombre de personnes infectées est n et l'environnement est j, la probabilité d'avoir une nouvelle infection entre t et t+dt, avec dt infiniment petit, est \(\,a_j\, n(1-n/N)\, dt\). Supposons que le taux de guérison b > 0 d'un individu soit le même dans les deux environnements. La probabilité d'une nouvelle guérison dans la population est alors \(b\, n\, dt\,\) entre t et t+dt. Ce modèle a été étudié par (Artalejo et coll., 2013) mais pas dans la limite où la taille N de la population devient grande. C'est d'ailleurs un cas particulier de processus de naissance et de mort dans un environnement markovien (Cogburn et Torrez, 1981).
Définissons \[Q=\left (\begin{array}{cc} -q_1 & q_2 \\ q_1 & -q_2 \end{array} \right ),\quad u_1=\frac{q_2}{q_1+q_2}\, ,\quad u_2=\frac{q_1}{q_1+q_2}\, ,\quad R_0=\frac{a_1 u_1+a_2 u_2}{b}\, .\] Alors \(Q\) est le générateur infinitésimal, tandis que \(u_1\) (resp. \(u_2\)) est la proportion du temps passé dans l'environnement 1 (resp. 2). Pour le modèle linéarisé, à savoir le processus linéaire de naissance et de mort dans un environnement aléatoire de paramètres \(\,a_j\) et \(b\), (Bacaër et Ed-Darraz, 2014) note qu'il y a extinction presque sûrement si et seulement si \(R_0 \leq 1\). Pour le modèle non-linéaire SIS en revanche, il y a extinction quelle que soit la valeur du paramètre \(\,R_0\). Cependant, lorsque la population N est grande, le temps moyen jusqu'à extinction est grand si \(\,R_0 > 1\) et petit si \(R_0 < 1\). Si \(\,T_{n,j}\,\) est le temps moyen avec au départ n personnes infectées dans l'environnement j, alors pour \(1\leq n\leq N\), \begin{align} T_{n,1}&=\frac{1 + a_1 n(1-n/N) T_{n+1,1} + bn T_{n-1,1}+q_1 T_{n,2}}{a_1n(1-n/N)+bn+q_1}\, ,\tag{1}\\ T_{n,2}&=\frac{1 + a_2 n(1-n/N) T_{n+1,2} + bn T_{n-1,2}+q_2 T_{n,1}}{a_2n(1-n/N)+bn+q_2}\, .\tag{2} \end{align} De plus \(T_{0,1}=T_{0,2}=0\). L'objectif de cet article est d'étudier dans le cas surcritique, c'est-à-dire si \(\,R_0 > 1\), le comportement du temps moyen jusqu'à extinction lorsque la taille de la population N devient grande.
Dans un environnement constant avec un taux de contact a avec \(\,R_0=\frac{a}{b} > 1\), (Doering et coll., 2005, tableau 1) montre que le temps moyen jusqu'à extinction partant d'une fraction infectée de la population x=n/N croît quand \(\,N\to \infty\), indépendamment de x, comme \(\frac{a}{(a-b)^2} \sqrt{\frac{2\pi}{N}}\, e^{cN}\), où \(c=b/a-1-\log(b/a)\). Autrement dit, le temps moyen croît à peu près exponentiellement avec N. (Bacaër, 2015) suggère un résultat similaire lorsque l'environnement est périodique, même s'il n'y a pas de formule explicite pour le paramètre de croissance c.
Dans un environnement aléatoire surcritique, c'est-à-dire avec \(R_0 > 1\,\), l'article qui suit suggère que deux cas doivent être distingués : un cas fortement surcritique où \(a_1 > a_2 > b\) et un cas faiblement surcritique où \(a_1 > b > a_2\). Dans le cas fortement surcritique où \(\,a_1 > a_2 > b\,\), on conjecture que le temps moyen jusqu'à extinction croît à peu près exponentiellement avec N avec un paramètre \(\,c_2=b/a_2-1-\log(b/a_2)\). Plus exactement, le logarithme de ce temps moyen, divisé par N, converge vers \(\,c_2\). Le comportement asymptotique est donc le même que si l'environnement restait bloqué dans l'état 2, c'est-à-dire celui le moins favorable à la propagation de l'épidémie et celui dans lequel l'extinction a lieu préférentiellement.
En revanche, si \(a_1 > b > a_2\) et \(R_0 > 1\,\), alors on conjecture que le temps moyen jusqu'à extinction croît comme \(N^\omega\) avec \begin{equation} \omega=\frac{q_2}{b-a_2}-\frac{q_1}{a_1-b}\, . \tag{3} \end{equation} Dans ce cas, \(R_0 > 1\) équivaut à \(\omega > 0\). De manière intuitive, il arrive de temps en temps que l'on reste dans l'état 2 pendant une durée très longue. La probabilité que cette durée soit supérieure à τ est \(e^{-q_2\tau}\). Dans l'état 2, le temps moyen d'extinction pour N grand est de l'ordre de \(\tau\simeq \frac{\log N}{b-a_2}\) (Doering et coll., 2005); cela se devine aussi avec l'équation de quasi-extinction \(\,e^{-(b-a_2)\tau}=1/N\). Donc finalement la probabilité d'extinction lors d'une période dans l'état 2 est de l'ordre de \(e^{-q_2\tau}\simeq N^{-\frac{q_2}{b-a_2}}\). Ceci suggère que le temps moyen jusqu'à extinction est de l'ordre de grandeur de l'inverse, c'est-à-dire \(\,N^{\frac{q_2}{b-a_2}}\). Selon notre analyse, l'ordre de grandeur est en réalité \(\,N^\omega\) avec ω donné par (3).
Notons d'ailleurs que si \(q_1\) et \(q_2\) sont multipliés par \(1+\varepsilon\) avec \(\varepsilon > 0\,\), alors \(R_0\) reste inchangé mais \(\omega\) est multiplié par \(1+\varepsilon\) : dans ce modèle, une variabilité environnementale accrue tend à augmenter le temps moyen d'extinction.
Cette loi en \(N^\omega\) semble pouvoir se généraliser au cas d'un environnement avec J états si \[a_1 > a_2 > \ldots > a_J,\quad b > a_J,\quad R_0 > 1.\] On a \[R_0=(\sum_{j=1}^J a_j u_j)/b\] si Q est le générateur infinitésimal et si u est l'unique vecteur avec \[Qu=0,\quad \sum_{j=1}^J u_j = 1,\quad u_j>0\quad \forall j\] (Bacaër et Ed-Darraz, 2014). Notons A et B les matrices diagonales \(\,\mathrm{diag}(a_1,\ldots,a_J)\) et \(\mathrm{diag}(b,\ldots,b)\). Considérons la borne spectrale \[\mu(s)=\max \left \{ \Re(\lambda);\ \lambda \in \sigma(Q-s(A-B)) \right \},\] où \(\sigma(\cdot)\) désigne le spectre d'une matrice et \(\Re(\cdot)\,\) la partie réelle d'un nombre complexe. On montre \[\exists !\ \omega> 0,\quad \mu(\omega)=0.\] On conjecture alors que le temps moyen jusqu'à extinction croît comme \(N^\omega\). Dans le cas particulier où \(\,a_j\neq b\) pour tout j, le nombre ω est simplement la valeur propre de plus grande partie réelle de la matrice \(\,(A-B)^{-1}Q\). Cette matrice et l'expression de sa valeur propre ω donnée par (3) pour I=2 se trouvent déjà chez (Sawyer et Slatkin, 1981, équations (14) et (20)) pour un modèle de population sans stochasticité démographique dans le cas sous-critique (\(R_0 < 1\)); dans ce cas, le temps moyen jusqu'à extinction croît cependant comme le logarithme de N.
Plusieurs auteurs ont trouvé une loi de puissance pour le temps moyen jusqu'à extinction dans des modèles de population en environnement aléatoire brownien (Ludwig, 1976 ; Leigh, 1981 ; Lande, 1993). Ils utilisent comme point de départ une équation de diffusion. Cependant (Gaveau et coll., 1996) et (Doering et coll., 2005) ont montré que cette équation conduit à une formule inexacte pour le paramètre c. En effet, cette équation ne représente pas toujours bien la queue de la distribution quasi-stationnaire, qui est précisément la partie la plus importante pour étudier le processus d'extinction. On notera cependant que (Kamenev et coll., 2008) ont abordé le problème de l'extinction pour des populations dans un environnement aléatoire avec un bruit coloré en utilisant des intégrales de chemin.
La section 2 présente la distribution quasi-stationnaire du modèle. La section 3 utilise la méthode de Brillouin, Kramers et Wentzel (BKW) pour obtenir des approximations valables dans les zones du paramètre x=n/N où la distribution varie rapidement. La section 4 utilise une autre approximation dans la zone où la distribution varie lentement. La section 5 utilise une équation de diffusion pour raccorder les deux précédentes approximations: les fonctions hypergéométriques confluentes de Kummer et Tricomi remplacent ici la fonction d'erreur de Gauss utilisée notamment par (Meerson et Sasorov, 2008). La section 6 estime la valeur propre associée avec la distribution quasi-stationnaire.
Aucune de ces approximations n'ayant été obtenue de manière rigoureuse, la section 7 présente néanmoins des simulations numériques qui semblent confirmer la valeur numérique des exposants pour la loi exponentielle dans le cas fortement surcritique et pour la loi de puissance dans le cas faiblement surcritique. La section 8 ajoute quelques remarques. En particulier, on compare dans le régime faiblement surcritique le cas d'un environnement markovien et celui d'un environnement périodique avec la même proportion du temps dans un état favorable ou défavorable: le premier conduit à une une loi de puissance pour le temps moyen jusqu'à extinction, le second à une loi exponentielle. La section 9 considère le cas d'une chaîne de Markov avec un nombre fini d'états et évoque d'autres généralisations. Enfin la section 10 se penche sur les environnements à la fois périodiques et stochastiques, mimant ainsi les saisons et la variabilité climatique.
Considérons la probabilité qu'il y ait n personnes infectées, dans l'environnement j, au temps t : \(\,p_{n,j}(t)\). Alors \begin{align} \frac{dp_{n,1}}{dt} =& -\left [a_1 n (1-\tfrac{n}{N}) + b\, n + q_1\right ] p_{n,1}+b(n+1) p_{n+1,1}\nonumber\\ &+a_1 (n-1) (1-\tfrac{n-1}{N}) p_{n-1,1} + q_2\, p_{n,2} \tag{4}\\ \frac{dp_{n,2}}{dt} =& -\left [a_2 n (1-\tfrac{n}{N}) + b\, n + q_2\right ] p_{n,2}+b(n+1) p_{n+1,2}\nonumber\\ &+a_2 (n-1) (1-\tfrac{n-1}{N}) p_{n-1,2} + q_1\, p_{n,1} .\tag{5} \end{align} Définissons


Définissons
Le cas \(x > x_1=1-b/a_1\). Avec \(\,R_0 > 1\), on conjecture que \(\lambda\to 0\) si \(N\to +\infty\). On vérifiera a posteriori, comme l'ont fait par exemple (Meerson et Sasorov, 2008) pour un modèle différent, que c'est bien le cas. Le côté gauche de (6)-(7) peut ainsi être négligé. Pour \(\,x > x_1\,\), cherchons une approximation BKW (Bender et Orszag, 1978) de la forme \[\pi_{n,1}=e^{-NS(x)-\Sigma(x)},\quad \pi_{n,2}=\frac{c(x)}{N}\, e^{-NS(x)-\Sigma(x)}\] où \(x=n/N\). Un développement de Taylor d'ordre 2 pour \(S(x)\) et d'ordre 1 pour \(\Sigma(x)\) suggère que \[\pi_{n\pm1,1}\simeq e^{-NS(x)\mp S'(x)-\frac{S''(x)}{2N}-\Sigma(x) \mp \frac{\Sigma'(x)}{N}}.\] On obtient en remplaçant dans (6) et en simplifiant par \(\,e^{-NS(x)-\Sigma(x)}\) \begin{align*} 0\simeq &\, a_1 N (x-\tfrac{1}{N}) (1-x+\tfrac{1}{N}) e^{S'(x)-\frac{S''(x)}{2N}+\frac{\Sigma'(x)}{N}} - a_1 N x(1-x) \\ & + bN (x+\tfrac{1}{N}) e^{-S'(x)-\frac{S''(x)}{2N}-\frac{\Sigma'(x)}{N}} -bNx-q_1+q_2 \frac{c(x)}{N}\, . \end{align*} Les expressions en O(N) donnent \[0\simeq N x \left [e^{S'(x)}-1\right ] \left [a_1(1-x)-b e^{-S'(x)}\right ].\] Le premier terme entre crochets n'est nul que pour les fonctions constantes \(S(x)\). Choisissons la solution qui annule le second terme entre crochets \[e^{S'(x)}=\frac{b}{a_1(1-x)},\] c'est-à-dire \[ S(x)=s_1(x)=x \log (b/a_1) + x + (1-x) \log(1-x)\] à une constante additive près. Ceci implique \(S''(x)=\frac{1}{1-x}\). La fonction \(\,\Sigma(x)\) s'obtient avec les expressions en O(1): \begin{align*} 0\simeq &\, a_1 N \left [x(1-x)+\frac{2x-1}{N}\right ] e^{S'(x)} \left [1+\frac{S''(x)}{2N}+\frac{\Sigma'(x)}{N} \right ] - a_1 N x(1-x) \\ &+bN(x+\tfrac{1}{N}) e^{-S'(x)} \left [1-\frac{S''(x)}{2N} - \frac{\Sigma'(x)}{N} \right ] - bNx -q_1\, . \end{align*} En remplaçant \(S(x)\) par son expression, on obtient \begin{align*} \Sigma'(x)&=\frac{1}{x}-\frac{1/2}{1-x} + \frac{q_1}{a_1-b} \left ( \frac{1}{x-x_1} - \frac{1}{x} \right )\, ,\\ \Sigma(x)&=\sigma_1(x)= \log\left (x\, \sqrt{1-x} \left [ \frac{x-x_1}{x}\right ]^{\frac{q_1}{a_1-b}}\right )\, . \end{align*} La fonction \(c(x)\) dans \(\pi_{n,2}\,\) s'obtient à partir de (7). La forme de \(\pi_{n,2}\,\) a été choisie pour assurer la balance entre les différentes expressions. En effet, l'ordre le plus élevé donne \[ 0 \simeq \frac{c(x)}{N} \left \{Na_2x(1-x) \left [e^{S'(x)}-1\right ] + bNx \left (e^{-S'(x)}-1\right ) \right \}+q_1\, .\] En remplaçant \(S(x)\) par son expression, on obtient \[c(x) \simeq \frac{q_1}{(a_1-a_2) x (x-x_1)}\, .\] En résumé, on conjecture pour \(x > x_1\), \begin{equation} \pi_{n,1} \simeq k_1\, e^{-Ns_1(x)-\sigma_1(x)},\quad \pi_{n,2}\simeq \frac{q_1\, \pi_{n,1}}{N(a_1-a_2)x(x-x_1)}\, ,\tag{10} \end{equation} pour une certaine constante \(k_1\). Considérons en particulier le comportement de \(\,\pi_{n,1}\) et de \(\pi_{n,2}\) pour \(x > x_1\) et \(x\) proche de \(x_1\). Définissons \(\,c_1=b/a_1-1-\log(b/a_1)\). On a \(\,s_1'(x_1)=0\). Un développement de Taylor donne \[s_1(x)\simeq s_1(x_1)+s_1''(x_1) (x-x_1)^2/2\simeq -c_1+\frac{a_1}{2b} (x-x_1)^2.\] Ainsi \begin{equation} \pi_{n,1} \simeq k_1 \frac{e^{Nc_1-N\frac{a_1}{2b} (x-x_1)^2}\, x_1^{\frac{q_1}{a_1-b}-1} }{\sqrt{1-x_1}\, (x-x_1)^{\frac{q_1}{a_1-b}} } \, ,\quad \pi_{n,2} \simeq \frac{q_1\, \pi_{n,1}}{N(a_1-a_2)x_1(x-x_1)}\, .\tag{11} \end{equation}
Le cas \(x < x_2=1-b/a_2\) si \(a_1 > a_2 > b\). Symétriquement, cherchons une solution si \(\,a_2 > b\) \[\pi_{n,2}=e^{-NS(x)-\Sigma(x)},\quad \pi_{n,1}=\frac{c(x)}{N}\, e^{-NS(x)-\Sigma(x)}\] pour \(x < x_2=1-b/a_2\). Le système (6)-(7) conduit, comme ci-dessus, à \[S(x)=s_2(x)=x \log (b/a_2) + x + (1-x) \log(1-x) \] à une constante additive près, tandis que \[\Sigma(x)=\sigma_2(x)= \log\left (x\, \sqrt{1-x} \left [ \frac{x_2-x}{x}\right ]^{\frac{q_2}{a_2-b}}\right ) ,\quad c(x) \simeq \frac{q_2}{(a_1-a_2) x (x_2-x)}\, .\] En résumé, on conjecture pour \(x < x_2\), \begin{equation} \pi_{n,2} \simeq k_2\, e^{-Ns_2(x)-\sigma_2(x)},\quad \pi_{n,1}\simeq \frac{q_2\, \pi_{n,2}}{N(a_1-a_2)x(x_2-x)}\, , \tag{12} \end{equation} pour une certaine constante \(k_2\). Pour \(\,x < x_2\) et \(x\) proche de \(x_2\), \begin{equation}\tag{13} \pi_{n,2} \simeq k_2 \frac{e^{Nc_2-N\frac{a_2}{2b} (x_2-x)^2}\, x_2^{\frac{q_2}{a_2-b}-1} }{\sqrt{1-x_2}\, (x_2-x)^{\frac{q_2}{a_2-b}} } \, ,\quad \pi_{n,1} \simeq \frac{q_2\, \pi_{n,2}}{N(a_1-a_2)x_2(x_2-x)}\, . \end{equation}
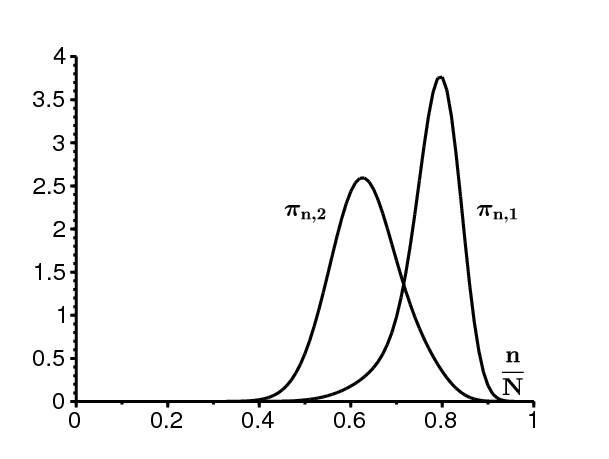
Les figures 2 et 3 montrent \(-(\log {\pi}_{n,1})/N\) et \(-(\log {\pi}_{n,2})/N\) en fonction de \(n/N\) pour \(1\leq n\leq N,\) avec \(\,\pi_{n,i}\) calculé en utilisant le système (6)-(7). Les figures montrent aussi les approximations (10) et (12) en bleu foncé et rouge. La constante \(\,k_1\) dans (10) est choisie de sorte que \(\pi_{n,1}\) coïncide avec son approximation pour n=N-1. La constante \(\,k_2\) dans (12) est déterminée par \(k_1\) comme cela est expliqué dans la section 5 ci-dessous.

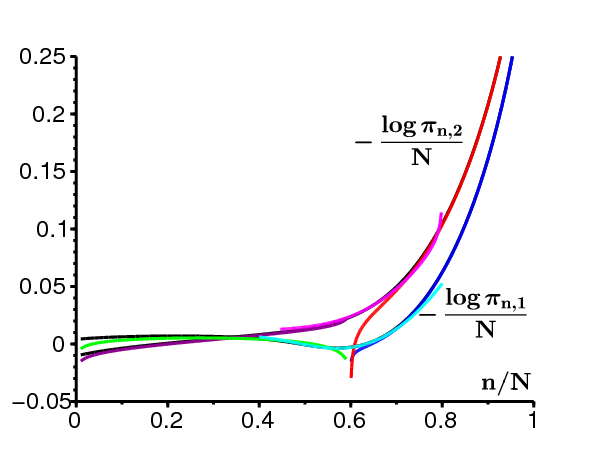
On cherche une approximation de \(\pi_{n,1}\) et \(\pi_{n,2}\) pour \(x_2 < x < x_1\) si \(a_1 > a_2 > b\, \) et pour \(0 < x < x_1\) si \(a_1 > b > a_2\). Sur ces intervalles, \(S(x)=0\). Considérons le système (6)-(7) et essayons directement l'approximation continue \(\,\pi_{n,1}\simeq y(x)\), \(\pi_{n,2}\simeq z(x)\), avec \(x=n/N\). Un développement de Taylor donne \[\pi_{n\pm 1,1}=y(x\pm1/N)\simeq y(x) \pm\frac{y'(x)}{N}+\frac{y''(x)}{2N^2}.\] Avec λ ≈ 0, cela conduit à l'approximation diffusive \begin{align} 0\simeq &\frac{d}{dx} \bigl [ (bx-a_1x(1-x)) y\bigr ] - q_1 y + q_2 z + \frac{1}{2N} \frac{d^2}{dx^2} \bigl [(a_1x(1-x)+bx)y\bigr ]\tag{14}\\ 0\simeq &\frac{d}{dx} \bigl [ (bx-a_2x(1-x)) z\bigr ] - q_2 z + q_1 y + \frac{1}{2N} \frac{d^2}{dx^2} \bigl [(a_2x(1-x)+bx)z\bigr ].\tag{15} \end{align} En négligeant 1/N, on obtient les équations \begin{align} 0\simeq &\frac{d}{dx} \bigl [ (bx-a_1x(1-x)) y(x)\bigr ] - q_1 y(x) + q_2 z(x) \tag{16}\\ 0\simeq &\frac{d}{dx} \bigl [ (bx-a_2x(1-x)) z(x)\bigr ] - q_2 z(x) + q_1 y(x) \, ,\tag{17} \end{align} qui sont de la même forme que les équations (29)-(30) de (Slatkin, 1978). En additionnant les équations (16) et (17), on trouve \[\frac{d}{dx} \bigl [(bx-a_1x(1-x)) y(x)+(bx-a_2x(1-x)) z(x)\bigr ]\simeq 0\, .\] La fonction entre crochets est donc constante. Parce que x est en facteur, cela suggère en faisant \(x\to 0\) que cette constante est égale à zéro: \begin{equation}\tag{18} (bx-a_1x(1-x)) y(x)+(bx-a_2x(1-x)) z(x)\simeq 0\, . \end{equation} Cela permet d'exprimer \(y(x)\) en fonction de \(z(x)\). En remplaçant dans (17), on obtient après quelques manipulations \begin{align} \frac{1}{z(x)} \frac{dz}{dx} &\simeq \frac{q_1}{bx-a_1 x(1-x)} + \frac{q_2}{bx-a_2x(1-x)}-\frac{b-a_2(1-2x)}{bx-a_2x(1-x)}\, ,\nonumber\\ z(x) &\simeq \frac{C}{bx-a_2x(1-x)} \left (\frac{a_1(1-x)-b}{x} \right ) ^{\frac{q_1}{a_1-b}} \left (\frac{b-a_2(1-x)}{x} \right )^{\frac{q_2}{a_2-b}} \tag{19} \end{align} pour une certaine constante C. Cette approximation est représentée en violet sur la figure 3. La constante C est déterminée par \(\,k_1\,\) comme cela est indiqué dans la section 5 ci-dessous. Puis les équations (18) et (19) montrent que \begin{equation}\tag{20} y(x)\simeq \frac{C}{a_1x(1-x)-bx} \left (\frac{a_1(1-x)-b}{x} \right ) ^{\frac{q_1}{a_1-b}} \left (\frac{b-a_2(1-x)}{x} \right )^{\frac{q_2}{a_2-b}}\, . \end{equation} Cette approximation est représentée en vert sur la figure 3. Si \(\,x \simeq x_1\) avec \(x < x_1\,\), on obtient \begin{align} y(x) &\sim \frac{C}{a_1 x_1}\, \left (\frac{a_1}{x_1} \right )^{\frac{q_1}{a_1-b}} \left (\frac{b-a_2(1-x_1)}{x_1}\right )^{\frac{q_2}{a_2-b}} (x_1-x)^{\frac{q_1}{a_1-b}-1}\, . \tag{21} \end{align} Si \(a_1 > b > a_2\,\), on trouve pour x ≈ 0 \begin{align} y(x)&\sim C\, (a_1-b)^{\frac{q_1}{a_1-b}-1}\, (b-a_2)^{\frac{q_2}{a_2-b}}\, x^{-1+\frac{q_2}{b-a_2}-\frac{q_1}{a_1-b}}\tag{22}\\ z(x)&\sim C\, (a_1-b)^{\frac{q_1}{a_1-b}}\, (b-a_2)^{\frac{q_2}{a_2-b}-1}\, x^{-1+\frac{q_2}{b-a_2}-\frac{q_1}{a_1-b}}\, .\tag{23} \end{align} Rappelons que \(R_0=\frac{a_1 q_2 + a_2 q_1}{b(q_1+q_2)} > 1\) équivaut à \(\frac{q_2}{b-a_2} > \frac{q_1}{a_1-b}\,\) dans ce cas. En particulier, l'intégrale de \(\,z(x)\) au voisinage de \(0^+\,\) est convergente. Si \(\,a_1 > a_2 > b\), alors (19) montre \begin{equation}\tag{24} z(x) \simeq \frac{C}{a_2\, x_2}\, \left (\frac{a_1(1-x_2)-b}{x_2} \right )^{\frac{q_1}{a_1-b}} \left (\frac{a_2}{x_2} \right )^{\frac{q_2}{a_2-b}} (x-x_2)^{\frac{q_2}{a_2-b}-1} \, \end{equation} près de \(x_2\) avec \(x > x_2\).
La situation près de \(x_1\). Près de \(\,x=x_1\) et \(x=x_2\,\), la diffusion dans (14)-(15) ne peut plus être négligé. L'analyse des zones de transition en \(\,x_1\) et \(x_2\,\) doit permettre de relier la constante C dans (21) et (24) avec les constantes \(\,k_1\) de (10) et \(k_2\,\) de (12). Définissons \(\, x=x_1+\xi_1/\sqrt{N}\). Alors le coefficient de la dérivée d'ordre 1 dans (14) peut être approché par un développement de Taylor d'ordre 1 \begin{align*} &0 \simeq (a_1-b) \frac{d}{d\xi_1} \left [\xi_1 y\right ] - q_1 y + q_2 z + b (1-b/a_1) \frac{d^2y}{d\xi_1^2} \, . \end{align*} On néglige \(q_2 z\) devant \(q_1 y\) si \(x\simeq x_1\) : \[0 \simeq \frac{b}{a_1} \frac{d^2 y}{d\xi_1^2} +\xi_1 \, \frac{dy}{d\xi_1}+\left (1- \frac{q_1}{a_1-b}\right ) y\, .\] Avec \begin{equation}\tag{25} \eta_1 = \xi_1 \sqrt{\frac{a_1}{2b}}\, ,\quad y(\eta_1)=e^{-\eta_1^2} Y(\eta_1) \end{equation} on a l'équation différentielle de Hermite \[0 \simeq \tfrac{1}{2} \frac{d^2Y}{d\eta_1^2} - \eta_1 \frac{dY}{d\eta_1} - \frac{q_1}{a_1-b} Y\, .\] On cherche une solution sous la forme d'une série entière \[Y(\eta_1)=\sum_{n=0}^\infty w_n \eta_1^n\,.\] On obtient la relation de récurrence \[w_{n+2} = \frac{2 (n+2\alpha_1)}{(n+2)(n+1)}\, w_n\, ,\] où \(\alpha_1=\frac{q_1/2}{a_1-b}\). On a ainsi deux solutions linéairement indépendantes \[ Y(\eta_1)= \gamma_1\, \Phi(\alpha_1,\tfrac{1}{2};\eta_1^2)+\gamma_2\, \eta_1\, \Phi(\alpha_1+\tfrac{1}{2},\tfrac{3}{2};\eta_1^2)\, , \] où \(\gamma_1\) et \(\gamma_2\) sont des constantes et \[\Phi(\alpha,\beta;z)=\sum_{n=0}^\infty \frac {\alpha^{(n)} z^n} {\beta^{(n)} n!},\quad \alpha^{(0)}=1,\quad \alpha^{(n)}=\alpha(\alpha+1)(\alpha+2)\cdots(\alpha+n-1)\] est la fonction hypergéometrique confluente de Kummer. D'après (Maroni, 1997, équation (93)), on a \(\Phi(\alpha,\beta;z)\sim \frac{\Gamma(\beta)}{\Gamma(\alpha)}\, e^{z}\, z^{\alpha-\beta}\) si \(z\to +\infty\), où Γ est la fonction Gamma d'Euler. Ainsi \[Y(\eta_1) \sim e^{\eta_1^2} |\eta_1|^{2\alpha_1-1} \left ( \frac{\gamma_1\, \Gamma(\frac{1}{2})}{\Gamma(\alpha_1)} - \frac{\gamma_2\, \Gamma(\frac{3}{2})}{\Gamma(\alpha_1+\frac{1}{2})} \right ),\quad \eta\to -\infty.\] Donc \(y(\eta_1)=e^{-\eta_1^2} Y(\eta_1)\) a le même comportement asymptotique que (21) lorsque \(\eta_1\to -\infty\, \), pourvu que \begin{equation}\tag{26} \left [\sqrt{\frac{N a_1}{2b}}\, \right ]^{\frac{q_1}{a_1-b}-1} \left ( \frac{\gamma_1\, \Gamma(\frac{1}{2})}{\Gamma(\alpha_1)} - \frac{\gamma_2\, \Gamma(\frac{3}{2})}{\Gamma(\alpha_1+\frac{1}{2})} \right ) = \frac{C\, (b-a_2(1-x_1))^{\frac{q_2}{a_2-b}}}{a_1^{1-\frac{q_1}{a_1-b}}\, x_1^{1+\frac{q_1}{a_1-b}+\frac{q_2}{a_2-b}}} \, . \end{equation} Si au contraire \(\eta_1\to +\infty\), (11) suggère que \(Y(\eta_1)\) doit se comporter comme une certaine constante multipliée par \(\eta_1^{-2\alpha_1}\). La théorie des fonctions hypergéométriques confluentes (Maroni, 1997) montre qu'il faut imposer \begin{equation}\tag{27} \gamma_1=\frac{\Gamma(\frac{1}{2})}{\Gamma(\alpha_1+\frac{1}{2})}\, K,\quad \gamma_2=\frac{\Gamma(-\frac{1}{2})}{\Gamma(\alpha_1)}\, K \end{equation} pour une certaine constante K pour obtenir un tel comportement asymptotique. En effet, on a alors \begin{equation}\tag{28} Y(\eta_1)=K \left ( \frac{\Gamma(\frac{1}{2})}{\Gamma(\alpha_1+\frac{1}{2})}\, \Phi(\alpha_1,\tfrac{1}{2};\eta_1^2) + \frac{\Gamma(-\frac{1}{2})}{\Gamma(\alpha_1)} \, \eta_1\, \Phi(\alpha_1+\tfrac{1}{2},\tfrac{3}{2};\eta_1^2) \right )\, , \end{equation} c'est-à-dire \(Y(\eta_1)=K\, \Psi(\alpha_1,\tfrac{1}{2};\eta_1^2)\) pour \(\eta_1 > 0\), où \(\Psi(\alpha,\beta;z)\) est la fonction hypergéometrique confluente de Tricomi définie par \[\Psi(\alpha,\beta;z)=\frac{\Gamma(1-\beta) }{\Gamma(\alpha-\beta+1)}\, \Phi(\alpha,\beta;z) +\frac{\Gamma(\beta-1)}{\Gamma(\alpha)}z^{1-\beta}\Phi(\alpha-\beta+1,2-\beta;z)\, .\] D'après (Maroni, 1997, équation (90)), on a bien \(\Psi(\alpha,\beta;z) \sim z^{-\alpha}\) si \(z\to +\infty\). Donc \(\,Y(\eta_1) \sim K\, \eta_1^{-2\alpha_1}\) si \(\eta_1 \to +\infty\).
L'équivalent de \(e^{-\eta_1^2} Y(\eta_1)\) coïncide alors avec (11) pourvu que \begin{equation}\tag{29} K \left [\sqrt{\frac{N a_1}{2b}}\, \right ]^{-\frac{q_1}{a_1-b}} = k_1\, \frac{e^{Nc_1}}{\sqrt{1-x_1}}\, x_1^{\frac{q_1}{a_1-b}-1} \, . \end{equation} En résumé, les relations (26), (27) et (29) déterminent \(K\), \(\gamma_1\), \(\gamma_2\) et \(C\) en fonction de \(k_1\). En particulier, parce que \(\,\Gamma(-\tfrac{1}{2})=-2\sqrt{\pi}\), \(\Gamma(\tfrac{1}{2})=\sqrt{\pi}\) et \(\Gamma(\tfrac{3}{2})=\tfrac{\sqrt{\pi}}{2}\), l'équation (26) donne \begin{equation}\tag{30} \left [\sqrt{\frac{N a_1}{2b}}\, \right ]^{\frac{q_1}{a_1-b}-1} \!\!\! \frac{2\pi\, K}{\Gamma(\alpha_1) \Gamma(\alpha_1+\frac{1}{2})} = \frac{C\, (b-a_2(1-x_1))^{\frac{q_2}{a_2-b}}}{a_1^{1-\frac{q_1}{a_1-b}}\, x_1^{1+\frac{q_1}{a_1-b}+\frac{q_2}{a_2-b}}}\, . \end{equation} Une forme alternative peut être obtenue en utilisant la formule de Legendre-Gauss \(\Gamma(\alpha_1) \Gamma(\alpha_1+\frac{1}{2})=\frac{\sqrt{\pi}}{2^{2\alpha_1-1}} \Gamma(2\alpha_1)\).
La situation près de \(x_2\). Si \(\,a_2 > b\,\), on fait une analyse similaire avec (15) près de \(x=x_2=1-b/a_2\). On néglige \(q_1 y\) devant \(q_2 z\). Si \[x=x_2+\tfrac{\xi_2}{\sqrt{N}}, \quad \eta_2=\xi_2 \sqrt{\tfrac{a_2}{2b}}, \quad z(\eta_2)=e^{-\eta_2^2} Z(\eta_2),\quad \alpha_2=\tfrac{q_2/2}{a_2-b},\] alors \begin{equation}\tag{31} Z(\eta_2)= \delta_1\, \Phi(\alpha_2,\tfrac{1}{2};\eta_2^2)+\delta_2\, \eta_2\, \Phi(\alpha_2+\tfrac{1}{2},\tfrac{3}{2};\eta_2^2) \end{equation} où \(\delta_1\) et \(\delta_2\,\) sont des constantes. Le comportement pour \(\,\eta_2\to +\infty\) coïncide avec (24) pourvu que \begin{equation}\tag{32} \left [\sqrt{\frac{N a_2}{2b}}\, \right ]^{\frac{q_2}{a_2-b}-1} \!\!\! \left ( \frac{\delta_1\, \Gamma(\frac{1}{2})}{\Gamma(\alpha_2)} + \frac{\delta_2\, \Gamma(\frac{3}{2})}{\Gamma(\alpha_2+\frac{1}{2})} \right ) = \frac{C\, [a_1(1-x_2)-b]^{\frac{q_1}{a_1-b}}}{ a_2^{1-\frac{q_2}{a_2-b}} \ x_2^{1+\frac{q_1}{a_1-b}+\frac{q_2}{a_2-b}}}\, . \end{equation} Définissons \begin{equation}\tag{33} \delta_1=\frac{\Gamma(\frac{1}{2})}{\Gamma(\alpha_2+\frac{1}{2})}\, \hat{K},\quad \delta_2=- \frac{\Gamma(-\frac{1}{2})}{\Gamma(\alpha_2)}\, \hat{K} \end{equation} pour une certaine constante \(\hat{K}\) (noter le signe moins pour \(\delta_2\)). Alors \(\,Z(\eta_2)=\hat{K}\, \Psi(\alpha_2,\frac{1}{2};\eta_2^2)\) si \(\eta_2 < 0\). Donc \(e^{-\eta_2^2} Z(\eta_2) \sim \hat{K}\, e^{-\eta_2^2} |\eta_2|^{-2\alpha_2}\) pour \(\eta_2 \to -\infty\). Ceci coïncide avec (13) pourvu que \begin{equation}\tag{34} \hat{K} \left [\sqrt{\frac{N a_2}{2b}}\, \right ]^{-\frac{q_2}{a_2-b}} = k_2\, \frac{e^{Nc_2} }{\sqrt{1-x_2}}\, x_2^{\frac{q_2}{a_2-b}-1}\, . \end{equation} Comme ci-dessus, (32) et (33) donnent \begin{equation}\tag{35} \left [\sqrt{\frac{N a_2}{2b}}\, \right ]^{\frac{q_2}{a_2-b}-1} \!\!\! \frac{2\pi\, \hat{K}}{\Gamma(\alpha_2) \Gamma(\alpha_2+\frac{1}{2})} = \frac{C\, [a_1(1-x_2)-b]^{\frac{q_1}{a_1-b}}}{a_2^{1-\frac{q_2}{a_2-b}}\, x_2^{1+\frac{q_1}{a_1-b}+\frac{q_2}{a_2-b}}}\ . \end{equation} Ainsi les constantes \(k_2\), \(\hat{K}\), \(\delta_1\) et \(\delta_2\,\) sont déterminées par la constante C.
Rappelons que \(M\pi=\lambda \pi\). En additionnant toutes les lignes de ce système d'équations, on obtient \(\, \lambda \sum_{n=0}^N (\pi_{n,1}+\pi_{n,2})=0\). Mais \(\,\lambda < 0\). Donc \[\sum_{n=0}^N (\pi_{n,1}+\pi_{n,2})=0.\] Les deux premières lignes du système sont \begin{align*} \lambda \, \pi_{0,1} &= -q_1\, \pi_{0,1} + q_2\, \pi_{0,2} + b \, \pi_{1,1}\, ,\\ \lambda \, \pi_{0,2} &= -q_2\, \pi_{0,2} + q_1 \, \pi_{0,1} + b \, \pi_{1,2}\, . \end{align*} En les additionnant, on trouve \begin{equation}\tag{36} \lambda = b\, \frac{\pi_{1,1}+\pi_{1,2}}{\pi_{0,1}+\pi_{0,2}} = -b\, \frac{\pi_{1,1}+\pi_{1,2}}{\sum_{n=1}^N (\pi_{n,1}+\pi_{n,2})}\, . \end{equation}
Considérons d'abord le cas où \(a_1 > b > a_2\) avec \(R_0 > 1\). Alors (19) montre \[\frac{1}{N} \sum_{n=1}^N \pi_{n,2} \simeq \int_0^{x_1} z(x)\, dx \simeq \kappa_1\, C \] où \(\kappa_1\) est une constante positive indépendante de \(N\). En utilisant le fait que le pic de \(\,\pi_{n,1}\) est proche de \(\,x=n/N=x_1\) et les relations (25), (28) et (30), on trouve \begin{equation}\tag{37} \frac{1}{N} \sum_{n=1}^N \pi_{n,1} \simeq \int_{-\infty}^{+\infty} y(\eta_1)\, d\eta_1\ \frac{dx}{d\eta_1}\simeq \kappa_2 \frac{K}{\sqrt{N}} \simeq \kappa_3\, C \, N^{-\frac{q_1/2}{a_1-b}}\, , \end{equation} où les \(\kappa_j\,\) (ci-dessus et ci-dessous) sont encore des constantes positives, qui sont indépendantes de N. Ainsi le terme dominant pour N grand dans le dénominateur de (36) est celui avec \(\,\pi_{n,2}\). Au numérateur, \(\,\pi_{1,1}\simeq y(\tfrac{1}{N})\) et \(\pi_{1,2}\simeq z(\tfrac{1}{N})\) où \(y(x)\) et \(z(x)\) sont donnés par (22)-(23), on obtient que \[\lambda\simeq - \kappa_4\, \frac{(\tfrac{1}{N})^{\frac{q_2}{b-a_2}-\frac{q_1}{a_1-b}-1}}{N } \simeq - \kappa_4\, N^{-\frac{q_2}{b-a_2}+\frac{q_1}{a_1-b}} \, .\] Autrement dit, \(-1/\lambda\,\) croît avec N comme une loi de puissance, dont l'exposant est \[\omega=\frac{q_2}{b-a_2}-\frac{q_1}{a_1-b} > 0,\] ainsi qu'annoncé dans l'introduction. On remarque d'ailleurs que ω converge vers \(\,+\infty\) si \(a_2\) converge vers b par valeurs inférieures.
Considérons maintenant le cas où \(a_1 > a_2 > b\). Pour simplifier, introduisons la notation \(f \approx g\) (à ne pas confondre avec le symbole informel \(\simeq\) utilisé ci-dessus) si \((\log f)/N - (\log g)/N\to 0\) si \(N\to +\infty\). En particulier \(\,N^\beta\approx 1\) pour tout β. Alors (12) avec x=1/N montre que \(\,\pi_{1,1}\approx \pi_{1,2}\). De plus, \[\pi_{1,2}\approx k_2\, e^{-Ns_2(1/N)}\approx k_2\, e^{-s_2'(0)}\approx k_2.\] Par ailleurs, le pic de \(\pi_{n,1}\) est proche de \(x=n/N=x_1\) alors que celui de \(\pi_{n,2}\) est proche de \(x_2\). Ainsi (37) est encore valable et montre \[\frac{1}{N} \sum_{n=1}^N \pi_{n,1} \approx C,\] tandis que (31), (33) et (35) donnent \[\frac{1}{N} \sum_{n=1}^N \pi_{n,2} \simeq \int_{-\infty}^{+\infty} z(\eta_2)\, d\eta_2\ \frac{dx}{d\eta_2}\simeq \kappa_5 \frac{\hat{K}}{\sqrt{N}} \simeq \kappa_5 \, C\, N^{-\frac{q_2/2}{a_2-b}} \approx C\, . \] Mais (34) et (35) montrent \[C \approx \hat{K} \approx k_2\, e^{Nc_2}.\] Ainsi (36) donne \(-\lambda\approx e^{-Nc_2}\) et \(-1/\lambda\approx e^{Nc_2}\). Finalement, \(\,-1/\lambda\) croît à peu près exponentiellement avec un paramètre \(c_2\).
Le système linéaire (8)-(9) peut être résolu avec la méthode numérique présentée par (Artalejo et coll., 2013). La méthode n'utilise que des matrices carrées d'ordre 2 et réduit l'instabilité numérique. Rappelons que \(\,q_1=q_2=1\) et \(b=2\).
Premier exemple: \(a_1 > a_2 > b\). Prenons \(a_1=10\) et \(a_2=5\). La figure 4a montre \(\,T_{n,1}\) et \(T_{n,2}\) en fonction de \(x=n/N\). La figure 4b suggère que le temps moyen jusqu'à extinction, partant par exemple de N personnes infectées dans l'environnement 1, croît à peu près exponentiellement: \(\,T_{N,1} \approx e^{cN}\). Une régression linéaire donne \(\,c\simeq 0.32\). Noter que \(c_1\simeq 0.81\) et \(c_2\simeq 0.32\), ce qui suggère bien que \(c=c_2\).

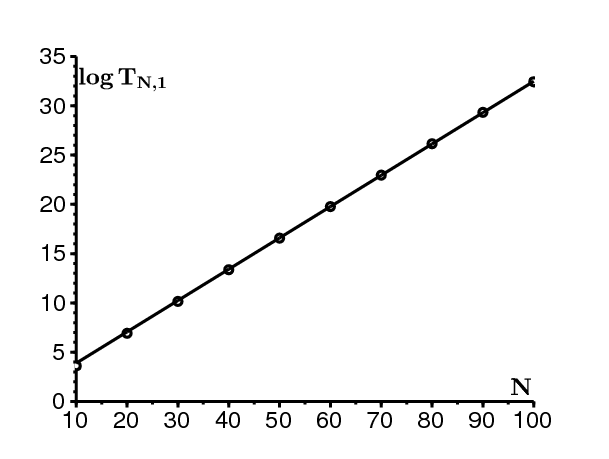
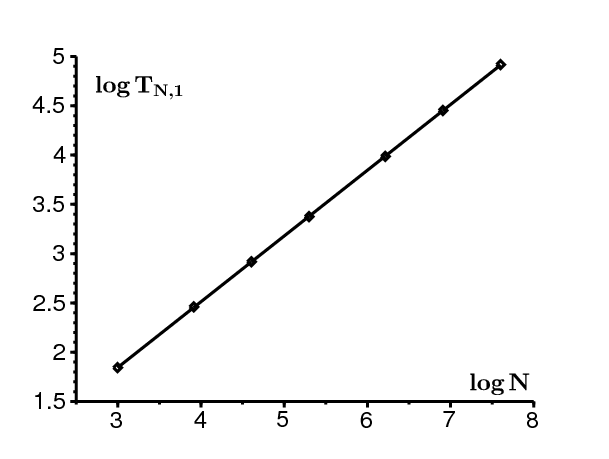
Deuxième exemple : \(a_1 > b > a_2\) et \(R_0 > 1\). Prenons \(a_1=5\) et \(a_2=1\). Donc \(\,R_0=1.5 > 1\). La figure 5a montre \(\,T_{n,1}\) et \(T_{n,2}\) en fonction de \(x=n/N\). La figure 5b montre \(\log T_{N,1}\) en fonction de \(\log N\). On obtient une ligne droite suggérant une loi de puissance \(T \sim \kappa\, N^\omega\). La pente, obtenue par régression linéaire, est \(\omega\simeq 0.67\). Dans ce cas, on a \(\frac{q_2}{b-a_2}-\frac{q_1}{a_1-b}=1-\frac{1}{3}=\frac{2}{3}\), ce qui correspond bien à la pente mesurée.
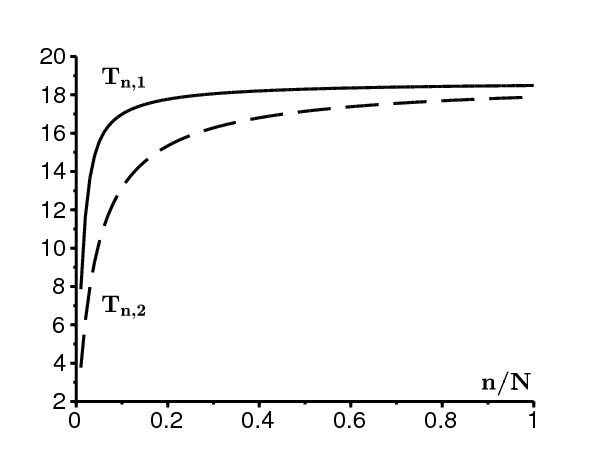
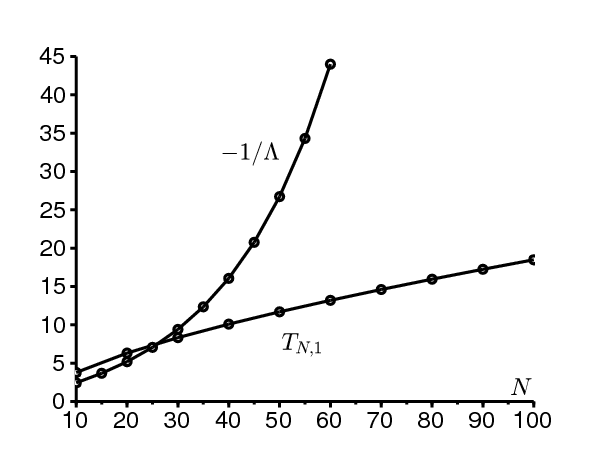
Pour mettre en évidence la différence entre un environnement aléatoire et un environnement périodique, reprenons le cas où \(a_1=5\) et \(a_2=1\,\), tandis que \(q_1=q_2=1\) et \(b=2\). Alors \(\,u_1=u_2=0.5\) : l'environnement passe en moyenne la moitié du temps dans l'état 1, l'autre moitié dans l'état 2. La figure 6 remontre d'un côté comment \(T_{N,1}\) croît en fonction de N comme une loi de puissance. D'un autre côté, considérons le même modèle SIS mais dans un environnement périodique (Bacaër, 2015) : choisissons \(\,T=\frac{1}{q_1}+\frac{1}{q_2}\), \(a(t)=a_1\) pour \(0 < t < u_1T\,\), et \(a(t)=a_2\) pour \(u_1T < t < T\). Pour ce modèle, \(e^{\Lambda T}\,\) est le multiplicateur de Floquet associé au processus d'extinction. La figure 6 montre comment \(\,-1/\Lambda\) croît exponentiellement avec \(N\).
Les équations de champ moyen. Il n'est peut-être pas inutile de rappeler en suivant (Bacaër et Ed-Darraz, 2014) que les équations de champ moyen \begin{align*} \frac{dI_1}{dt} &= a_1 I_1 (1-\tfrac{I_1}{N}) - b I_1 -q_1 I_1 + q_2 I_2\\ \frac{dI_2}{dt} &= a_2 I_2 (1-\tfrac{I_2}{N}) - b I_2 -q_2 I_2 + q_1 I_1, \end{align*} une fois linéarisées près de l'état d'équilibre (0,0), conduisent à la matrice jacobienne \[\left (\begin{array}{cc} a_1-b-q_1 & q_2\\ q_1 & a_2-b-q_2 \end{array} \right ).\] Mais on peut avoir en même temps
Autre limite. Les résultats obtenus considèrent que les paramètres \(\,q_j\), \(a_j\,\) et \(b\,\) sont fixés tandis que N converge vers l'infini. Les choses sont évidemment différentes si par exemple \(q_1\) et \(q_2\) convergent vers l'infini, avec un rapport constant \(q_1/q_2\). Le modèle se rapproche alors d'un modèle homogénéisé en environnement constant avec un paramètre de contact moyenné \(\bar{a}=a_1 u_1+a_2 u_2\).
Le cas sous-critique. On n'a pas abordé le cas sous-critique \(\,R_0 < 1\) avec \(a_1 > b > a_2\) ou bien \(b > a_1 > a_2\). Le comportement du temps moyen jusqu'à extinction est alors sensiblement le même que dans un environnement constant: partant d'une fraction fixe de la population qui est infectée, le temps moyen est de l'ordre de \(\,\log N\,\) (Doering et coll., 2005). Partant d'une fraction infectée 1/N, le temps moyen converge au contraire vers une limite. Dans le cas d'un environnement aléatoire, c'est aussi ce que suggèrent les simulations numériques.
Avec \(J\) états, rappelons que le générateur infinitésimal \(Q\) est tel que \(Q_{j,j}=-\sum_{i=1}^J Q_{i,j}\) pour tout \(j\). Supposons que cette matrice \(Q\) soit irréductible et que \(a_1 > a_2 > \cdots > a_J\). Si \(\,a_J > b\,\), alors le temps moyen jusqu'à extinction croît à peu près exponentiellement avec la taille N de la population, avec un taux \(\,c_J=b/a_J-1-\log(b/a_J)\). C'est en effet dans l'environnement J que l'extinction est la plus probable.
Si en revanche \(b > a_J\) et \(R_0 > 1\), notons \(\pi_{n,j}\simeq y_j(x)\) avec \(x=n/N\). Au voisinage de \(\,x=0\,\), le système (16)-(17) devient \begin{equation}\tag{38} 0 \simeq (b-a_j) \frac{d}{dx} (x\, y_j) + \sum_{k=1}^J Q_{j,k} y_k\, . \end{equation} En cherchant une solution \(y_j=\theta_j\, x^{\omega-1}\) avec \(\omega > 0\) et \(\theta_j > 0\) pour tout j, on trouve \[0 \simeq \omega (b-a_j) \theta_j + \sum_{k=1}^J Q_{j,k} \theta_k\, \] pour \(1\leq j\leq J\). Avec les notations de l'introduction, on a donc le problème de valeur propre généralisé \(Q\theta=\omega(A-B) \theta\,\), avec \(\theta=(\theta_1,\ldots,\theta_J)\).
On va montrer \[\exists !\ \omega > 0,\quad Q\theta=\omega(A-B) \theta, \quad \theta_j > 0\ \forall j.\] \(D=A-B\,\) est une matrice diagonale. Pour tout nombre réel s, \[\mu(s)=\max \left \{ \Re(\lambda);\ \lambda \in \sigma(Q-sD) \right \}.\] \(\,Q-sD\,\) a tous ses coefficients en dehors de la diagonale qui sont positifs ou nuls. De plus, cette matrice est irréductible. D'après un corollaire du théorème de Perron et Frobenius (Smith, 1995, corollaire 3.2), \(\mu(s)\) est une valeur propre simple de \(Q-sD\) (appelée valeur propre dominante) et il existe un vecteur propre \(\phi(s)\) dont toutes les composantes sont strictement positives tel que \[(Q-sD)\phi(s)=\mu(s) \phi(s).\] Ce vecteur propre est unique avec la normalisation \[\sum_{j=1}^J \phi_j(s)=1.\] D'après le même corollaire, l'existence d'un vecteur \(\,\theta\) avec \(\theta_j > 0\) pour tout \(j\) et \((Q-\omega D)\theta=0\) équivaut en fait à \(\mu(\omega)=0\). Il s'agit donc de montrer que l'équation \(\,\mu(\omega)=0\) avec \(\omega > 0\) a une unique solution.
Concernant l'existence, on remarque d'abord que le générateur infinitésimal \(Q\) correspond à \(s=0\) : on a \(\mu(0)=0\) et l'on note \(u=\phi(0)\,\) le vecteur propre à droite. Le vecteur ligne \(\,\mathbf{1}=[1,\ldots,1]\) est un vecteur propre à gauche de \(Q\) associé à la valeur propre 0. Ainsi \[\mathbf{1}u=\sum_{j=1}^J u_j=1.\] D'après le théorème de perturbation des valeurs propres simples, la fonction \(\,\mu(s)\) est dérivable en \(s=0\) et \[\mu'(0)=- \mathbf{1}Du.\] Mais \(\,R_0 > 1\) équivaut à \(\mathbf{1}Du=\sum_{j=1}^J (a_j-b) u_j > 0\). Donc \(\,\mu'(0) < 0\). Par ailleurs, on a \((Q/s-D)\phi(s)=(\mu(s)/s) \phi(s)\) pour tout \(s > 0\). Si \(\,s\to +\infty\), on a \(Q/s-D\to -D\). Par continuité du spectre, \[\mu(s)/s \to \max_j (-D_{j,j})=\max_j (b-a_j)=b-a_J > 0.\] Donc \(\,\mu(s)\to +\infty\) si \(s\to +\infty\). Parce que \(\,\mu(0)=0\) et \(\mu'(0) < 0\,\), on en déduit qu'il existe \(\omega > 0\) avec \(\mu(\omega)=0\).
Quant à l'unicité, remarquons tout d'abord que la fonction \(\mu(s)\,\) est convexe. En effet, pour tous les nombres réels \(\,\omega_1\), \(\omega_2\), et \(0 < \varepsilon < 1\), on voit que \(\mu(\varepsilon \omega_1+(1-\varepsilon)\omega_2)\) est la valeur propre dominante de la matrice \(Q-\varepsilon \omega_1 D-(1-\varepsilon)\omega_2 D\). D'après un théorème de (Cohen, 1981), cette valeur propre est inférieure ou égale à \(\,\varepsilon \mu(\omega_1)+(1-\varepsilon) \mu(\omega_2)\). Ceci prouve la convexité. Supposons maintenant qu'il existe \(\omega_1 > \omega_2 > 0\) avec \(\mu(\omega_1)=\mu(\omega_2)=0\). Parce que \(\mu(0)=0\) et parce que \(\mu(s)\) est convexe, on en déduit \(\mu(s)=0\) pour \(0\leq s\leq \omega_1\). Ceci contredit \(\,\mu'(0) < 0\).
\(A-B\) est une matrice inversible si \(\,a_j\neq b\,\) pour tout j. Ainsi \(\,Q\theta=\omega (A-B)\theta\) équivaut à \((A-B)^{-1}Q\theta=\omega \, \theta\). Donc \(\omega\) est la valeur propre de \((A-B)^{-1}Q\) dont la partie réelle est la plus grande.
Enfin l'équation (36) devient \[\lambda=-b\, \frac{\sum_{j=1}^J \pi_{1,j}}{\sum_{j=1}^J \sum_{n=1}^N \pi_{n,j}}\, .\] Au numérateur, on a \(\pi_{1,j}\simeq \theta_j (1/N)^{\omega-1}\). Au dénominateur, on a \[\sum_{n=1}^N \pi_{n,j}\simeq N \theta_j \int_0^1 x^{\omega-1}\, dx.\] Donc \(\,-1/\lambda\,\) croît avec N comme \(\,N^\omega\).
Il est sans doute possible de généraliser un tel résultat au cas où l'environnement est gouverné par exemple par une équation différentielle stochastique \[d\xi = f(\xi(t)) + \sigma dB(t).\] Définissons \(\,L^*\) l'opérateur différentiel \[(L^*u)(\xi)=\frac{\sigma^2}{2} \frac{d^2u}{d\xi^2}-\frac{d}{d\xi}(f(\xi)u(\xi)).\] On suppose que \(\,u(\xi)\) est une probabilité invariante: \[L^*u=0, \quad u > 0,\quad \int_{-\infty}^{+\infty} u(\xi)\, d\xi=1.\] Ainsi, dans le cas de l'équation de Langevin, on a \[f(\xi)=-k\, \xi,\quad k > 0, \quad u(\xi)=\sqrt{\frac{k}{\pi \sigma^2}}\, e^{-k \xi^2/\sigma^2}.\] On suppose que le taux de contact \(\,a(\cdot)\) est une fonction sur \(\mathbb{R}\) avec \(\min a(\cdot) < b\) et \[R_0=\left (\lim_{T\to \infty} \frac{1}{T} \int_0^T a(\xi(t))\, dt\right )/b=\left (\int_{-\infty}^{+\infty} a(\xi)\, u(\xi)\, d\xi\right )/b > 1.\] Le temps moyen d'extinction croît avec N comme \(N^\omega\), où \(\omega\) est l'unique nombre positif pour lequel l'opérateur différentiel \(L^*-\omega[a(\cdot)-b]\) ait une valeur propre principale égale à 0. Pour la convexité de cette valeur propre en fonction de \(\omega\,\), voir (Kato, 1982). Noter que l'opérateur adjoint de \(\,L^*\) est \[L=\frac{\sigma^2}{2} \frac{d^2}{d\xi^2}+f(\xi) \frac{d}{d\xi}\] et \(L\mathbf{1}=0\) si \(\mathbf{1}\) désigne la fonction constante égale à 1.
Revenons au cas d'un ensemble fini d'environnements. On suppose désormais que le générateur infinitésimal \(\,Q(t)\)
On conjecture que si \(a_1 > \ldots > a_J > b\,\), alors le temps moyen jusqu'à extinction croît encore exponentiellement avec N, avec un taux \[c_J=b/a_J-1-\log(b/a_J).\] Si en revanche \(\,a_J < b\) mais \(R_0 > 1\,\), l'approximation \(\pi_{n,j}(t)\simeq y_j(t,x)\) conduit à généraliser (38) au voisinage de \(x=0\) \[\frac{\partial y_j}{\partial t}\simeq (b-a_j) \frac{\partial}{\partial x}(x y_j) + \sum_{k=1}^J Q_{j,k}(t) y_k\, .\] Une solution de la forme \(y_j(t,x)=\theta_j(t) x^{\omega-1}\,\), avec une fonction \(\theta(t)=(\theta_j(t))\) \(\mathcal{T}\)-périodique, doit vérifier \[\frac{d\theta}{dt}=(Q(t)-\omega D) \theta(t)\, .\] Il existe un unique nombre réel \(\mu(\omega)\) pour lequel \(e^{\mu(\omega)\mathcal{T}}\) est le multiplicateur de Floquet dominant du système \[\frac{dX}{dt}=(Q(t)-\omega D)X.\] Cette matrice est une fonction périodique de période \(\mathcal{T}\) . Les coefficients hors diagonale sont positifs ou nuls. La matrice est irréductible sur un intervalle de t. On peut montrer qu'il existe un unique \(\, \omega > 0\) avec \(\mu(\omega)=0\). On utilise comme dans la section 9
Noter que la convexité de \(\mu(\omega)\,\) se démontre en généralisant simplement l'argument de (Cohen, 1981). On utilise
Parce que \[\lambda=-b \frac{\int_0^\mathcal{T} \sum_{j=1}^J \pi_{1,j}(t)\, dt}{\int_0^\mathcal{T} \sum_{j=1}^J \sum_{n=1}^N \pi_{n,j}(t)\, dt}\, ,\] on conclut comme avant que \(-1/\lambda\, \) croît sans doute avec N comme \(N^\omega\).
Cet article a été stimulé par une réunion à l' Instituto de Ciencias Matemáticas à Madrid en octobre 2014, par des cours à l'université de Tlemcen en mai 2015 et par un séminaire à l' Universidade Nova de Lisboa en juin 2015.