\(\mathrm{Institut\ de\
Recherche\ pour\ le\ D\acute{e}veloppement}\), Bondy, France
nicolas.bacaer@ird.fr
SACEMA, DST/NRF Centre d'excellence en analyse et modélisation épidémiologique, Université de Stellenbosch, Afrique du Sud
Lotka (1939) a étudié un modèle linéaire de population qui relie le nombre \(B(t)\,\) de naissances par unité de temps au temps t avec la fertilité \(\,f(x)\) et la mortalité \(\mu(x)\,\) à l'âge x : \begin{equation}\tag{1} B(t)=\int_0^\infty \phi(x) \, B(t-x)\, dx\, , \end{equation} où \(\phi(x)=f(x)\, e^{-\int_0^x \mu(y)\, dy}\). Il a montré que \(B(t)\) et la population totale croissent exponentiellement, comme \(e^{rt}\), où r est l'unique racine de l'équation \begin{equation}\tag{2} 1=\int_0^\infty \phi(x)\, e^{-r x}\, dx\, . \end{equation} Les analogues en temps discret de (1) et de (2) sont le modèle matriciel de population de Leslie et l'équation caractéristique de la matrice de Leslie (1945). Euler avait déjà étudié un cas particulier en 1760. On appelle souvent (2) « l'équation d'Euler-Lotka ». Lotka a utilisé la notation \begin{equation}\tag{3} R_0=\int_0^\infty \phi(x)\, dx\, . \end{equation} C'est le nombre moyen de descendants engendrés par un individu au cours de sa vie. \(R_0\,\) est la reproductivité. La population croît (\(r > 0\)) si \(R_0 > 1\). Elle décroît (\(r < 0\)) si \(R_0 < 1\). Le modèle (1) apparaît aussi dans l'étude de la stabilité linéaire de l'équilibre sans maladie des modèles épidémiques: la variable x représente alors le temps écoulé depuis l'infection et \(\,B(t)\) l'incidence des infections au début de l'épidémie (Diekmann et Heesterbeek, 2000).
De nombreuses populations animales ou végétales et de nombreuses maladies infectieuses présentent des fluctuations saisonnières. Ces fluctuations influencent à la fois le taux de croissance et la reproductivité. (Thieme, 1984 ; Jagers, 1985) remplacent le modèle (1) par \begin{equation}\tag{4} B(t)=\int_0^\infty \Phi(t,x) \, B(t-x)\, dx\, , \end{equation} où \(\Phi(t,x)\,\) est une fonction périodique de t de période T. Le taux de croissance r est alors l'unique nombre réel pour lequel le rayon spectral de l'opérateur intégral linéaire, sur l'espace des fonctions continues T-périodiques, est égal à 1 \begin{equation}\tag{5} u(t)\mapsto \int_0^\infty \Phi(t,x) \, e^{-r x}\, u(t-x)\, dx. \end{equation} (Bacaër et Guernaoui, 2006 ; Bacaër, 2007) ont suggéré que la reproductivité peut être définie de la même manière comme le rayon spectral de l'opérateur \[u(t)\mapsto \int_0^\infty \Phi(t,x) \, u(t-x)\, dx\] sur le même espace de fonctions continues T-périodiques. Comme avant, \(\,r > 0\) si \(R_0 > 1\) et \(r < 0\) si \(R_0 < 1\). Si \(\,\Phi(t,x)\) ne dépend pas de t, ces définitions et résultats se réduisent à ceux de Lotka.
Supposons maintenant que \begin{equation}\tag{6} \Phi(t,x)=[1+\varepsilon \cos(\omega t)]\, \phi(x), \end{equation} où \(\omega=2\pi/T\), \(|\varepsilon|\leq 1\) et \(\phi\geq 0\). On définit \[\xi = \inf \left \{ s \in \mathbb{R}, \quad \int_0^\infty \phi(x)\, e^{-s x}\, dx<+\infty \right \}.\] On suppose \(\xi < 0\). On définit \begin{equation}\tag{7} \phi_n(s)=\int_0^\infty \phi(x)\, e^{-s x -n \mathrm{i} \omega x}\, dx\, ,\quad n\in \mathbb{Z}, \quad s > \xi. \end{equation} Coale (1972, chapitre 6) a montré avec des notations différentes que \(r\simeq r_0+r_2\, \varepsilon^2\) pour \(\varepsilon\) petit, où \(r_0\) est défini implicitement et \(r_2\) explicitement par \begin{equation}\tag{8} 1=\phi_0(r_0)\quad , \quad r_2=- \frac{1}{2\, \phi_0'(r_0)} \, \mathrm{Re} \Bigl (\frac{1}{1/\phi_1(r_0)-1 }\Bigr )\, . \end{equation} Le symbole \(\mathrm{Re}(z)\,\) désigne la partie réelle du nombre complexe z. Dans (Bacaër, 2007), on a montré de la même manière que \(R_0\simeq R_{0,0}+ R_{0,2}\, \varepsilon^2\) pour \(\varepsilon\) petit, où \begin{equation}\tag{9} R_{0,0}=\phi_0(0) \quad , \quad R_{0,2}=\frac{\phi_0(0)}{2} \mathrm{Re} \Bigl (\frac{\phi_1(0)}{\phi_0(0)-\phi_1(0)}\Bigr )\, . \end{equation}
Dans le présent article, on adapte une méthode utilisée par (Just, 2000). On montre dans le cas particulier (6) que le taux de croissance et la reproductivité sont les plus grandes racines réelles d'équations avec des fractions continues \begin{eqnarray} \frac{1}{ \phi_0(r)} - 1 &=& 2\, \mathrm{Re}\ \cfrac{\varepsilon^2/4}{ \cfrac{1}{ \phi_1(r)} - 1 - \cfrac{\varepsilon^2/4}{ \cfrac{1}{ \phi_2(r)} - 1 - \cfrac{\varepsilon^2/4}{\cdots}}} \ ,\tag{10}\\ \frac{R_0}{ \phi_0(0)} - 1 &=& 2\, \mathrm{Re}\ \cfrac{\varepsilon^2/4}{ \cfrac{R_0}{\phi_1(0)} - 1 - \cfrac{\varepsilon^2/4}{ \cfrac{R_0}{\phi_2(0)} - 1 - \cfrac{\varepsilon^2/4}{\cdots}}}\ \tag{11} \end{eqnarray} pour tout \(|\varepsilon|\leq 1\). Noter une nouvelle fois sur le côté droit que l'on doit prendre la partie réelle de la fraction continue. On peut utiliser ces équations relativement simples pour calculer numériquement le taux de croissance et la reproductivité. Si l'on écrit par exemple \(\,r(\varepsilon)\) pour insister sur la dépendance du taux de croissance au paramètre, alors on verra qu'on a en général l'inégalité \(r(\varepsilon)\neq r(0)\) pour \(\varepsilon\neq 0\). Autrement dit, le seuil pour la croissance de la population (\(r > 0\)) ne peut être obtenu simplement en moyennant le coefficient périodique puisque ceci équivaudrait à prendre \(\varepsilon=0\). On illustre ce point avec un modèle épidémique SEIS/SEIR tiré de (Williams et Dye, 1997), qui comprend une période de latence fixe et une période infectieuse distribuée exponentiellement.
On obtient les équations (10) et (11) dans la section 2. À partir d'elles, on retrouve les formules approchées (8) et (9) dans la section 3. Le modèle épidémique SEIS/SEIR de (Williams et Dye, 1997) est pris en exemple dans la section 4. La conclusion mentionne d'autres exemples.
D'après (Thieme, 1984 ; Jagers, 1985), le rayon spectral de l'opérateur linéaire positif (5) est une fonction décroissante de r et le taux de croissance du modèle (4) est l'unique nombre réel tel que ce rayon spectral soit égal à 1. Par conséquent, le taux de croissance r est aussi le plus grand nombre réel tel qu'il existe une fonction périodique non triviale \(u(t)\) avec \begin{equation}\tag{12} \int_0^\infty \Phi(t,x)\, e^{-r x}\, u(t-x)\, dx = u(t),\quad \forall t. \end{equation} Considérons tout d'abord le cas où \(\,\Phi(t,x)=p(t)\, \phi(x)\,\) avec une fonction T-périodique \(\,p(t)\). Considérons les décompositions en série de Fourier \[p(t)=\sum_{n\in \mathbb{Z}} p_n \, e^{n \mathrm{i} \omega t}\, ,\quad u(t)=\sum_{n\in \mathbb{Z}} u_n \, e^{n \mathrm{i} \omega t}\, ,\] où \(\omega=2\pi/T\). Comme l'ont remarqué (Coale, 1972 ; Williams et Dye, 1997), l'équation (12) est équivalente à un système infini d'équations linéaires \begin{equation}\tag{13} \sum_{n \in \mathbb{Z}} p_{k-n}\, \phi_n(r)\, u_n=u_k\quad (k\in \mathbb{Z}), \end{equation} où \(\phi_n\) est défini par (7).
Considérons maintenant le cas particulier où \(p(t)=1+\varepsilon \cos(\omega t)\). Parce que \(\,p(t)=1+\frac{\varepsilon}{2}\, e^{\mathrm{i} \omega t} + \frac{\varepsilon}{2}\, e^{-\mathrm{i} \omega t}\,\), le système (13) s'écrit \begin{equation}\tag{14} \frac{\varepsilon}{2}\, \phi_{k-1}(r)\, u_{k-1} + \phi_k(r)\, u_k + \frac{\varepsilon}{2}\, \phi_{k+1}(r)\, u_{k+1} =u_k\quad (k\in \mathbb{Z})\, . \end{equation} On peut adapter la méthode utilisée par (Just, 2000) pour un système tridiagonal similaire. Réécrivons le système (14) \begin{equation}\tag{15} \frac{1}{ \phi_k(r)} - 1 = \frac{\varepsilon}{2}\, \frac{\phi_{k-1}(r)}{\phi_k(r)}\, \frac{u_{k-1}}{u_k} + \frac{\varepsilon}{2}\, \frac{\phi_{k+1}(r)}{\phi_k(r)}\, \frac{u_{k+1}}{u_k} \, . \end{equation} Si \(k=0\,\), cette équation s'écrit \begin{equation}\tag{16} \frac{1}{ \phi_0(r)} - 1 = \frac{\varepsilon^2/4}{\frac{\varepsilon}{2}\, \frac{\phi_{0}(r)}{\phi_{-1}(r)}\, \frac{u_{0}}{u_{-1}}} + \frac{\varepsilon^2/4}{\frac{\varepsilon}{2}\, \frac{\phi_{0}(r)}{\phi_{1}(r)}\, \frac{u_{0}}{u_{1}}} \, . \end{equation} Mais (15), avec k-1 ou k+1 remplaçant k, montre aussi \begin{eqnarray} \frac{\varepsilon}{2}\, \frac{\phi_{k}(r)}{\phi_{k- 1}(r)}\, \frac{u_{k}}{u_{k- 1}} &=& \frac{1}{ \phi_{k- 1}(r)} - 1 - \frac{\varepsilon^2/4}{\frac{\varepsilon}{2}\, \frac{\phi_{k- 1}(r)}{\phi_{k- 2}(r)}\, \frac{u_{k- 1}}{u_{k- 2}}} \, ,\tag{17}\\ \frac{\varepsilon}{2}\, \frac{\phi_{k}(r)}{\phi_{k+ 1}(r)}\, \frac{u_{k}}{u_{k+ 1}} &=& \frac{1}{ \phi_{k+ 1}(r)} - 1 - \frac{\varepsilon^2/4}{\frac{\varepsilon}{2}\, \frac{\phi_{k+ 1}(r)}{\phi_{k+ 2}(r)}\, \frac{u_{k+ 1}}{u_{k+ 2}}}\, . \tag{18} \end{eqnarray} Combinons (16) et (17)-(18) itérativement. On obtient les fractions continues \[ \frac{1}{ \phi_0(r)} - 1 = \cfrac{\varepsilon^2/4}{ \cfrac{1}{\phi_{-1}(r)} - 1 - \cfrac{\varepsilon^2/4}{ \cfrac{1}{\phi_{-2}(r)} - 1 - \cfrac{\varepsilon^2/4}{\cdots}}} + \cfrac{\varepsilon^2/4}{ \cfrac{1}{\phi_1(r)} - 1 - \cfrac{\varepsilon^2/4}{ \cfrac{1}{\phi_2(r)} - 1 - \cfrac{\varepsilon^2/4}{\cdots}}}\ . \] Parce que \(\phi_k(r)\) et \(\phi_{-k}(r)\,\) sont des nombres complexes conjugués, on arrive à « l'équation caractéristique » (10). Le taux de croissance r est la plus grande solution.
La preuve de (11) est similaire, en partant du problème \begin{equation}\tag{19} \int_0^\infty \Phi(t,x)\, u(t-x)\, dx = R_0\, u(t)\, . \end{equation} \(R_0\,\) est le plus grand nombre réel, pour lequel cette équation a une solution T-périodique non nulle. Pour le cas particulier \(\Phi(t,x)=(1+\varepsilon \cos(\omega t))\, \phi(x)\), l'équation (19) conduit à \[ \frac{\varepsilon}{2}\, \phi_{k-1}(0)\, u_{k-1} + \phi_k(0)\, u_k + \frac{\varepsilon}{2}\, \phi_{k+1}(0)\, u_{k+1} =R_0\, u_k\quad (k\in \mathbb{Z})\, ,\] et à l'équation (11).
En partant de (10)-(11), on peut retrouver facilement les approximations (8)-(9), qui ont été démontrées de manière plus compliquée dans (Coale, 1972 ; Bacaër, 2007).
Commençons avec le taux de croissance r. Cherchons le début d'un développement en série pour \(\,\varepsilon\) petit de la forme \(r\simeq r_0+r_1\, \varepsilon+r_2\, \varepsilon^2\). Si \(\,\varepsilon=0\,\), le côté droit de (10) s'annule et l'on obtient \(r_0\) comme (unique) solution de l'équation \(\phi_0(r_0)=1\), qui est bien sûr identique à l'équation (2) d'Euler-Lotka. Par ailleurs, le changement \(\,\varepsilon \mapsto -\varepsilon\) correspond à remplacer \(p(t)=1+\varepsilon \cos (\omega t)\) avec \(p(t-T/2)\). Or l'opérateur linéaire \[u(t) \mapsto \int_0^\infty \Phi(t-T/2,x)\, e^{-rx}\, u(t-x)\, dx\] sur l'espace des fonctions T-périodiques a les mêmes valeurs propres que l'opérateur linéaire (5), les fonctions propres étant juste décalées de T/2. Pour mettre en évidence la dépendance de r par rapport à ε, écrivons \(\,r(\varepsilon)\). Ainsi \(r(-\varepsilon)=r(\varepsilon)\) et \(r_1=0\). (Bacaër, 2007) a utilisé une argumentation similaire pour l'approximation de la reproductivité.
On a par conséquent \(r\simeq r_0+r_2\, \varepsilon^2\) et il reste à déterminer \(r_2\). Le taux de croissance r est une solution de l'équation implicite (10). Parce que \(\,\phi_0(r_0)=1\,\), on a \[\phi_0(r_0)-\phi_k(r_0)=\int_0^\infty \phi(x)\, e^{-r_0 x} (1-e^{-k \mathrm{i} \omega x})\, dx \neq 0\] pour tout entier \(k\geq 1\) (en supposant par exemple que la fonction \(\phi(x)\,\) est strictement positive au moins sur un petit intervalle). Donc \(\,\phi_k(r_0)\neq 1\) et \(1/\phi_k(r_0)-1\neq 0\) pour tout entier \(k\geq 1\). Pour ne garder que l'expression quadratique en ε du côté droit de l'équation (10), on remplace le dénominateur par son approximation d'ordre le plus bas. On remplace \(\,\phi_1(r)\) avec \(\phi_1(r_0)\). On néglige le reste quadratique en ε de la fraction continue. On obtient \begin{equation}\tag{20} \frac{1}{ \phi_0(r)} - 1 \simeq 2\, \mathrm{Re} \Bigl ( \frac{\varepsilon^2/4}{ 1/\phi_1(r_0) - 1}\Bigr )\, . \end{equation} Mais \[\phi_0(r)\simeq \phi_0(r_0+r_2\, \varepsilon^2) \simeq \phi_0(r_0)+r_2\, \varepsilon^2 \phi_0'(r_0) =1 +r_2\, \varepsilon^2 \phi_0'(r_0)\, . \] On utilise l'approximation pour \(\phi_0(r)\). On identifie les expressions quadratiques en ε dans (20). Cela donne \begin{equation} r_2=- \frac{1}{2\, \phi_0'(r_0)} \, \mathrm{Re} \Bigl (\frac{1}{1/\phi_1(r_0) -1 }\Bigr )\, , \end{equation} qui est équivalent à (8). Cette formule peut s'écrire sous une forme légèrement différente. En effet, avec \[c_1= \int_0^\infty \phi(x)\, e^{-r_0 x} \cos(\omega x)\, dx\, ,\quad s_1= \int_0^\infty \phi(x)\, e^{-r_0 x} \sin(\omega x)\, dx\, ,\] on a \(\phi_1(r_0)=c_1-\mathrm{i} s_1\). Donc \[r_2 = - \frac{1}{2\, \phi_0'(r_0)} \, \mathrm{Re} \Bigl (\frac{ c_1-\mathrm{i} s_1}{1-c_1+\mathrm{i} s_1 }\Bigr ) = - \frac{1}{2\, \phi_0'(r_0)} \, \frac{(1-c_1)\, c_1-s_1^2}{(1-c_1)^2+s_1^2}\, ,\] ce qui est essentiellement identique à la formule (6.27) de (Coale, 1972).
De même, \(R_0\simeq R_{0,0}+ R_{0,2}\, \varepsilon^2\) pour \(\varepsilon\,\) petit. D'après l'équation (3) ou l'équation (11) avec \(\,\varepsilon=0\,\), on a \(R_{0,0}=\phi_0(0)\). Pour ne garder du côté droit de l'équation (11) que l'expression quadratique en ε, on remplace le dénominateur par son approximation d'ordre le plus bas, en utilisant \(R_{0,0}=\phi_0(0)\). On néglige le reste de la fraction continue car il est quadratique en ε. On a \[\frac{R_0}{\phi_0(0)}-1\simeq 2\, \mathrm{Re} \Bigl ( \frac{\varepsilon^2/4}{\phi_0(0)/\phi_1(0)-1} \Bigr )\, . \] Ceci conduit à la formule (9).
Les modèles épidémiques appelés SEIR ou SEIS comportent une période de latence et un compartiment infectieux. Ils ont fait l'objet de nombreuses études mathématiques ou numériques lorsque de plus le taux de contact est périodique (Williams et Dye, 1997 ; Schwartz et Smith, 1983 ; Aron et Schwartz, 1984 ; Kuznetsov et Piccardi, 1994 ; Moneim et Greenhalgh, 2005 ; Ma et Ma, 2006). (Earn et coll., 2000) s'intéresse plus particulièrement à la rougeole, (Deguen et coll., 2000) à la varicelle, tandis que (Altizer et coll., 2006 ; Grassly et Fraser, 2006) présentent des revues générales. En dépit de son importance pour les questions d'éradication, seuls (Williams et Dye, 1997) et (Ma et Ma, 2006) ont étudié le seuil épidémique, qui dépend des équations linéarisées près de l'équilibre sans maladie. Les autres références se focalisent sur des situations endémiques, en cherchant du chaos ou en essayant d'estimer les paramètres, et ne mentionnent le problème que pour aussitôt se tourner vers des modèles plus simples sans période de latence. Toutes ces références prennent une période infectieuse distribuée exponentiellement.
(Williams et Dye, 1997) utilise des séries de Fourier pour étudier analytiquement le cas où la période de latence est une constante fixée et où le taux de contact est une fonction périodique arbitraire. Les auteurs affirment que le taux de croissance des équations linéarisées dépend du taux de contact périodique seulement par sa valeur moyenne. On montre ci-dessous pour le cas particulier d'un taux de contact sinusoïdal que ceci ne peut être vrai que pour des valeurs exceptionelles des paramètres. On aurait pu s'en rendre compte en utilisant la formule approchée (9) de (Coale, 1972).
(Ma et Ma, 2006) étudie numériquement un modèle SEIR qui est un système d'équations différentielles ordinaires, ce qui correspond à une période de latence distribuée exponentiellement, avec un taux de contact qui varie comme \(1+\varepsilon \cos \omega t\). Les auteurs ont trouvé que la valeur moyenne du taux de contact n'est pas suffisante pour déterminer le seuil épidémique. (Bacaër, 2007) a confirmé analytiquement cette observation en utilisant la formule approchée (9), qui montre dans cet exemple que la reproductivité, et donc aussi le seuil épidémique, dépend de ε.
(Just, 2000) utilise des séries de Fourier pour étudier une équation différentielle linéaire à retard, qui est formellement la même que la linéarisation d'un modèle SEIS ou SEIR avec une période de latence fixe. Cependant l'auteur a choisi la fonction \(\,c(t)=\varepsilon \cos(\omega t)\,\) pour le paramètre correspondant au taux de contact, ce qui ne convient pas dans le contexte de la dynamique des populations puique le taux de contact doit être positif (la motivation de (Just, 2000) est un problème d'ingénieur). L'auteur est arrivé pour le taux de croissance de son modèle à une équation caractéristique faisant intervenir des fractions continues semblables à (11).
Retournons au cas d'une période de latence fixe considéré par Williams et Dye (1997) et rappelons les différentes formulations possibles du même modèle SEIS. On remarque que le modèle SEIR conduit aux mêmes équations linéarisées près de l'équilibre sans maladie. Donc il a le même seuil épidémique.
La formulation avec une équation aux dérivées partielles comprend trois compartiments:
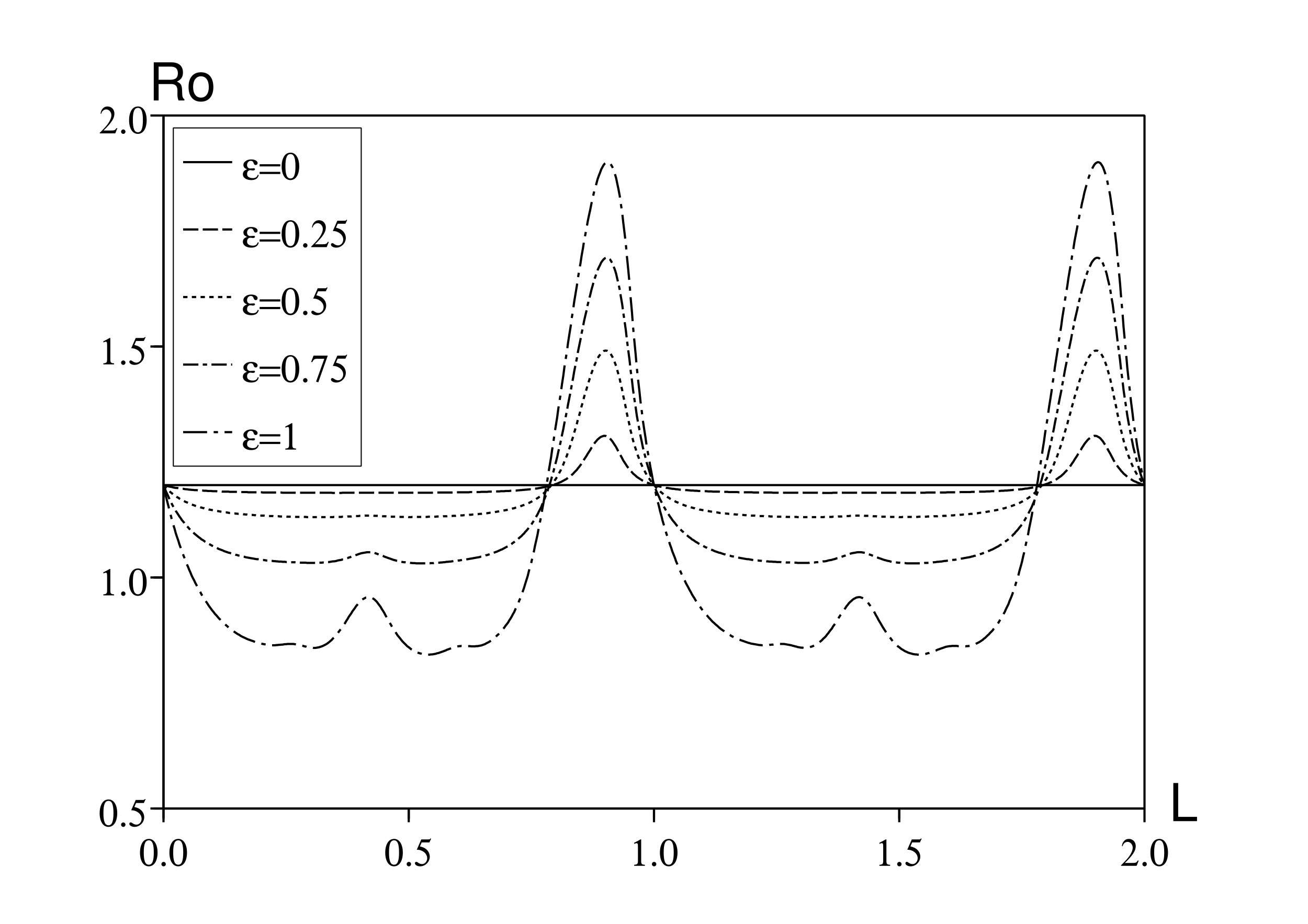
Supposons maintenant comme dans l'équation (6) que \(c(t)=c_0 [1+\varepsilon \cos(\omega t)]\), de sorte que \(\Phi(t,x)=( 1+\varepsilon \cos(\omega t))\, \phi(x)\) avec \(\phi(x)=c_0\, f(x)\). D'après la définition (7), on a \begin{equation}\tag{23} \phi_n(s)=c_0 \int_L^\infty e^{-a (x-L)}\, e^{-s x -n \mathrm{i} \omega x}\, dx = c_0\, \frac{e^{-s L - n \mathrm{i} \omega L}}{s + a + n \mathrm{i} \omega}\, . \end{equation} On peut ensuite résoudre les équations implicites (10) et (11) pour le taux de croissance et la reproductivité avec différentes valeurs des paramètres en utilisant une simple dichotomie. Noter par exemple que le dénominateur du côté droit de l'équation (10) peut être approché par le nombre complexe \(z_1\,\), avec l'algorithme itératif \[z_n=\frac{1}{\phi_n(r)}-1\, ,\quad z_{k-1}=\frac{1}{\phi_{k-1}(r)}-1-\frac{\varepsilon^2/4}{z_k}\quad (k=n,n-1,\dots,2).\] L'erreur introduite est très petite si n est pris assez grand. On a utilisé n=20 mais le résultat avec n=2 est déjà très proche. Par ailleurs, il a fallu faire attention avec la dichotomie car les équations (10) et (11) peuvent avoir plusieurs racines réelles: r et \(\,R_0\,\) sont les plus grandes. La figure 1 montre la reproductivité en fonction de la période de latence L, pour différentes valeurs de \(\,\varepsilon\,\). Pour T et \(\,a\,\), on a pris les mêmes valeurs que dans (Williams et Dye, 1997). Pour \(\,c_0\,\), on a pris \(c_0/a=\mbox{1,2}\) au lieu de \(c_0/a=\mbox{1,5}\,\) comme dans (Williams et Dye, 1997). Noter cependant avec l'équation (11) que si \(\,c_0\) est multiplié par une constante, alors \(R_0\) est multiplié par la même constante; donc l'allure de la figure 1 reste la même mais avec une échelle différente sur l'axe vertical.

Pour une valeur donnée de la période de latence, la reproductivité peut varier considérablement en fonction de ε. Pour \(\,\varepsilon=1\), une grande partie de la courbe pour \(R_0\) est en dessous de 1, c'est-à-dire sous le seuil épidémique, tandis que \(R_{0,0}=c_0/a\) (la valeur correspondant à \(\varepsilon=0\)) est au-dessus de ce seuil: moyenner le taux de contact prédirait un résultat faux. Voici quelques autres remarques:
Le deuxième point résulte de l'équation (11) et du fait que \[\phi_n(0)=c_0\, e^{-n \mathrm{i} \omega L}/(a+n \mathrm{i} \omega)\] reste inchangé quand L est remplacé par L+T. Intuitivement, un individu infecté fait l'expérience du même environnement après une période de latence L ou après une période de latence L+T ; il produit le même nombre de cas secondaires.
Le troisième point est également bien connu. Si \(\,L=0\,\), le modèle se réduit à un modèle SIS avec une période infectieuse distribuée exponentiellement. Dans ce cas particulier, la reproductivité s'obtient en moyennant le taux de contact (Bacaër et Guernaoui, 2006, §5 ; Bacaër, 2007, §5.1.1, et références incluses). En effet, \(R_0=c_0/a\) est une solution de (11) lorsque \(L=0\) car \(R_0/\phi_n(0)-1=R_0 (a+n \mathrm{i} \omega)/c_0-1=n \mathrm{i} \omega /a\) est purement imaginaire pour tout entier n≥ 1 : les côtés gauche et droit de (11) sont égaux à 0.
Pour comprendre le quatrième point, on utilise la formule approchée (9). On a \(\,R_0\simeq R_{0,0}+R_{0,2}\, \varepsilon^2\,\), avec \[R_{0,0}=\frac{c_0}{a}\quad ,\quad R_{0,2}=\frac{c_0}{2\, a}\, \mathrm{Re} \Bigl (\frac{1}{e^{\mathrm{i} \omega L} (1+\mathrm{i} \omega/a)-1} \Bigr )\, .\] Pour \(\varepsilon\) petit, \(R_0\) est une fonction croissante (ou décroissante) de \(\varepsilon\) si \(R_{0,2} > 0\) (ou \(R_{0,2} < 0\)). \(R_{0,2}=0\) si et seulement si \(e^{\mathrm{i} \omega\, L} (1+\mathrm{i} \omega/a) - 1\,\) est un nombre imaginaire pur. Cette condition s'écrit \[\cos(\omega L)-\frac{\omega}{a}\, \sin(\omega L)-1=0.\] On définit \(\,\psi \in (0,\pi/2)\) l'unique nombre réel avec \[\cos \psi= \frac{1}{\sqrt{1+(\omega/a)^2}}\, \quad , \quad \sin \psi = \frac{\omega/a}{\sqrt{1+(\omega/a)^2}}\, ,\] c'est-à-dire \(\psi=\arctan(\omega/a)\). Ce ψ dépend seulement du produit \(\,aT\). Donc \(R_{0,2}=0\) si et seulement si \[\cos(\omega L+\psi)= \cos(\omega L) \cos \psi - \sin(\omega L) \sin \psi =\frac{1}{\sqrt{1+(\omega/a)^2}}=\cos \psi\, ,\] c'est-à-dire \(\omega L + \psi = \pm \psi + 2k\pi\) pour \(k\in \mathbb{Z}\). Parce que \(\ \omega=2\pi/T\ \), on a \(R_{0,2}=0\) si \(L=k\, T\) ou \(L=(k-\psi/\pi)T\) pour \(k\in \mathbb{Z}\). En particulier, avec les valeurs numériques de la figure 1, \(\,R_{0,2}=0\) si \(L/T=1-\psi/\pi\simeq \mbox{0,794}\). Mais contrairement à ce que pourrait laisser croire la figure 1, les quatre courbes ne croisent pas la ligne horizontale \(R_0=c_0/a\) exactement en \(L/T=1-\psi/\pi\) mais très près.
De la même manière, la figure 2 montre le taux de croissance en fonction de la période de latence pour différentes valeurs de \(\varepsilon\) mais avec \(T\), \(c_0\) et \(a\,\) donnés comme précédemment. Le taux de croissance n'est pas une fonction périodique de L. Ce taux décroît en fonction de la période de latence, mais pas de manière monotone. Il y a des résonances entre L et T.
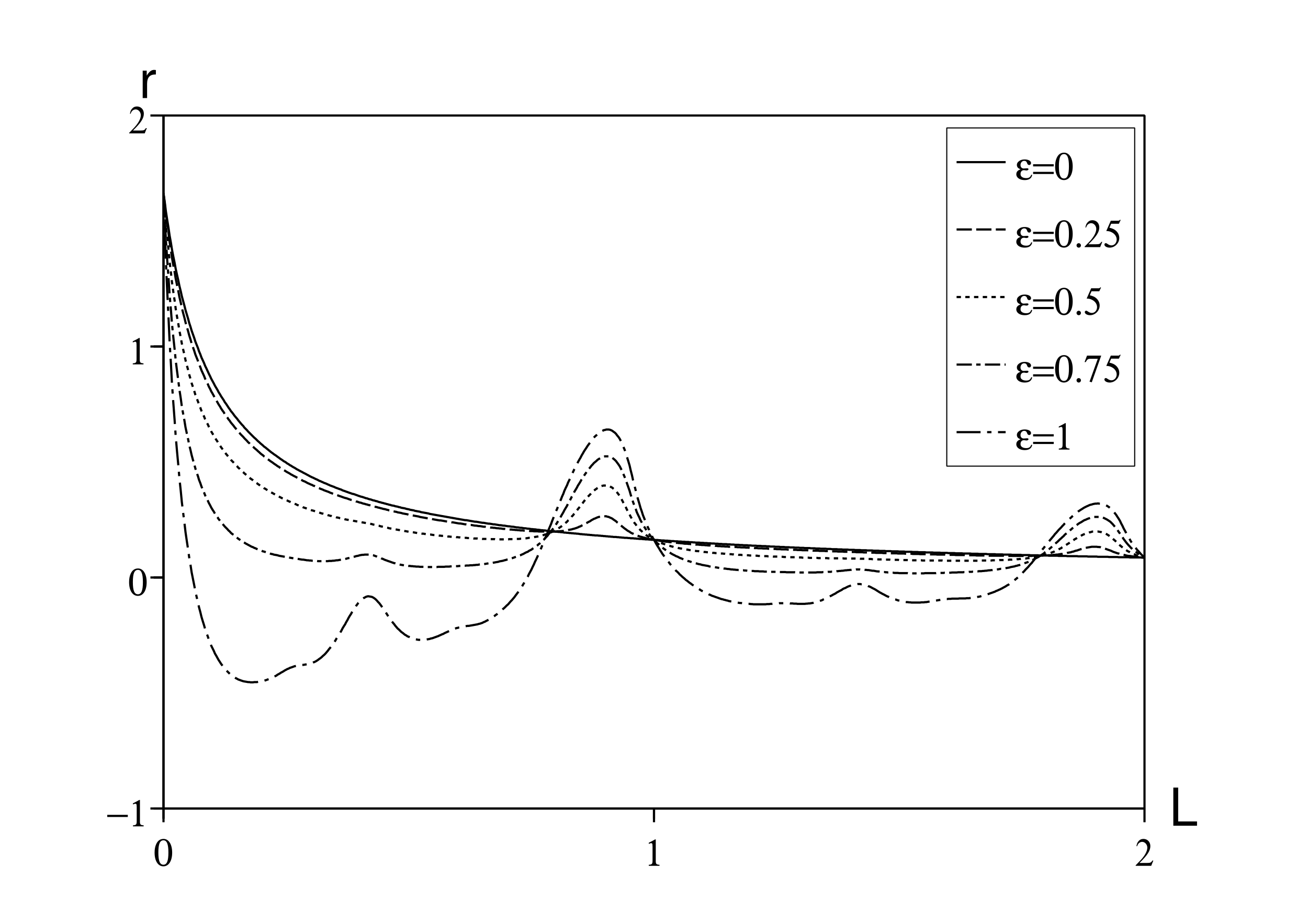
Cependant, \(r\) est encore indépendant de \(\varepsilon\,\) si L est un multiple de T, c'est-à-dire \(\,L=k\, T\) pour \(k=0,1,2\ldots\) En effet, rappelons que \(r_0\) est l'unique solution de l'équation \[\phi_0(r_0)=1 \Leftrightarrow c_0\, e^{-r_0 k T}/(r_0+a)=1\, .\] Donc \(r=r_0\) est aussi une solution de l'équation (10) car \[1/\phi_n(r)-1=(r_0+a+n \mathrm{i} \omega)\, e^{r_0 k T}/c_0-1=n \mathrm{i} \omega\, e^{r_0 k T}/c_0\] est purement imaginaire pour \(n\geq 1\) : les côtés gauche et droit de (10) sont nuls.
Pour une période de latence générale L, en utilisant (8) et (23), on a \(r\simeq r_0+r_2\, \varepsilon^2\) pour \(\varepsilon\) petit, avec \(r_0\) défini implicitement par \[ \phi_0(r_0)=1 \Leftrightarrow c_0\, e^{-r_0 L }/(r_0 + a)=1\, . \] \(r_2\,\) est donné par (8) et (23). Avec \begin{eqnarray*} &&\phi_1(r_0)=c_0\, \frac{e^{-r_0 L - \mathrm{i}\omega L}}{r_0+a+\mathrm{i}\omega}=c_0\, \frac{e^{-r_0 L}}{r_0+a}\times \frac{e^{-\mathrm{i}\omega L}}{1+\mathrm{i}\omega/(r_0+a)} = \frac{e^{-\mathrm{i}\omega L}}{1+\mathrm{i} \omega/(r_0+a)}\, ,\\ && \phi_0'(r_0)=- c_0\, \frac{e^{-r_0 L}}{r_0+a} \Bigl (L+\frac{1}{r_0+a}\Bigr ) = - \Bigl (L+\frac{1}{r_0+a}\Bigr )\, , \end{eqnarray*} on obtient \begin{eqnarray*} r_2&=&- \frac{1}{2\, \phi_0'(r_0)} \, \mathrm{Re} \Bigl (\frac{1}{1/\phi_1(r_0)-1 }\Bigr )\\ &=&\frac{1}{2 [L+1/(r_0+a)]} \, \mathrm{Re} \Bigl ( \frac{1}{e^{\mathrm{i} \omega L} [1+\mathrm{i} \omega / (r_0+a)] - 1} \Bigr )\, . \end{eqnarray*}
À part les modèles SEIS/SEIR mentionnés dans la section précédente, la stabilité linéaire de l'équilibre trivial de plusieurs autres modèles de population se réduit à l'équation (4), où \(\Phi(t,x)\,\) est donné par (6). C'est en particulier le cas pour les modèles épidémiques avec n compartiments infectés, où l'infection suit un cycle (\(I_1\to I_2\to \cdots I_n\to I_1\)) et avec seulement une fonction de contact sinusoïdale. Voir (Bacaër, 2007) et les références concernant le paludisme et le choléra. Le modèle épidémique SIS/SIR avec une période infectieuse fixe L et un taux de contact sinusoïdal correspond à \[\phi(x)=c_0\quad \forall x < L, \quad \phi(x)=0\quad \forall x > L.\] Dans ce cas, \[\phi_n(s)=c_0 (1-e^{-sL-n \mathrm{i} \omega L})/(s+n \mathrm{i} \omega).\] Comme dans la section précédente, la reproductivité et le taux de croissance sont indépendants de ε si L est un multiple de T. C'est un cas dégénéré, car il n'y a pas de raison que la période infectieuse ait quelque relation arithmétique avec la période des contacts, qui est ordinairement d'une semaine (moins de contacts durant les fins de semaines) ou une année (moins de contacts durant les vacances d'été pour les maladies infantiles, probabilité de transmission plus importante des maladies transmises par voie aérienne durant l'hiver). Le cas L=T a néanmoins reçu beaucoup d'attention dans la littérature mathématique (Cooke et Kaplan, 1976 ; Smith, 1977 ; Nussbaum, 1977 et 1978).
La signification plus générale de nos résultats est que la moyennisation de la reproductivité et du taux de croissance devrait être considérée comme exceptionnelle. À part les cas dégénérés semblables à ceux déjà mentionnés, la seule situation à notre connaissance où la moyennisation est correcte est celle avec un compartiment infectieux, une période infectieuse distribuée exponentiellement et pas de période de latence (Bacaër et Guernaoui, 2006, §5 ; Bacaër, 2007, §5.1.1, et ses références). La moyennisation n'est pas correcte pour toute déviation, par exemple deux compartiments infectieux comme pour les maladies à vecteurs (Bacaër, 2007, §4.1), ou une période infectieuse qui n'est pas distribuée exponentiellement (Bacaër, 2007, §5.1.1), ou une période de latence non nulle (Bacaër, 2007, §5.1.2).