\(\mathrm{Institut\ de\ Recherche\ pour\ le\ D\acute{e}veloppement}\), Bondy, France
nicolas.bacaer@ird.fr
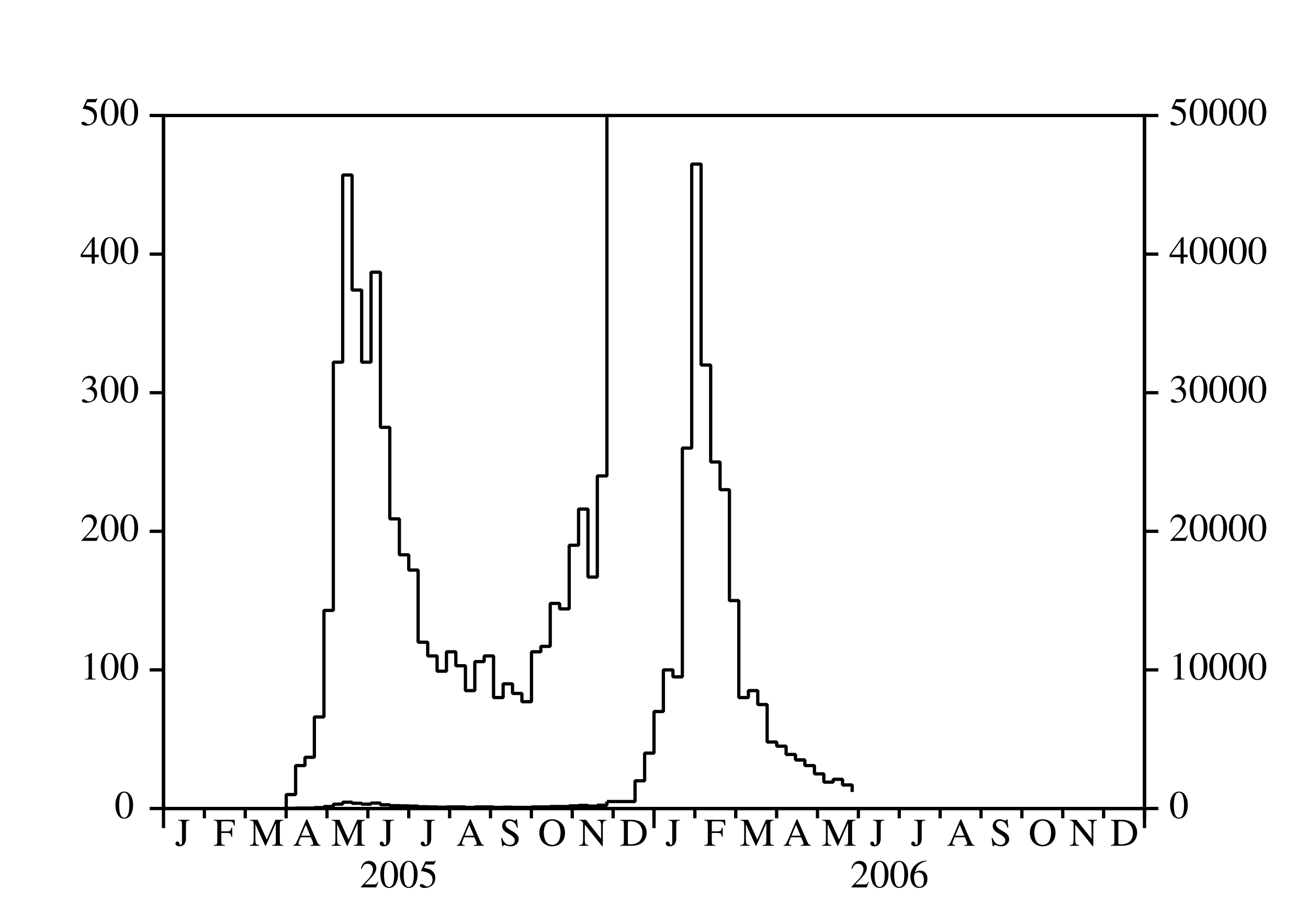
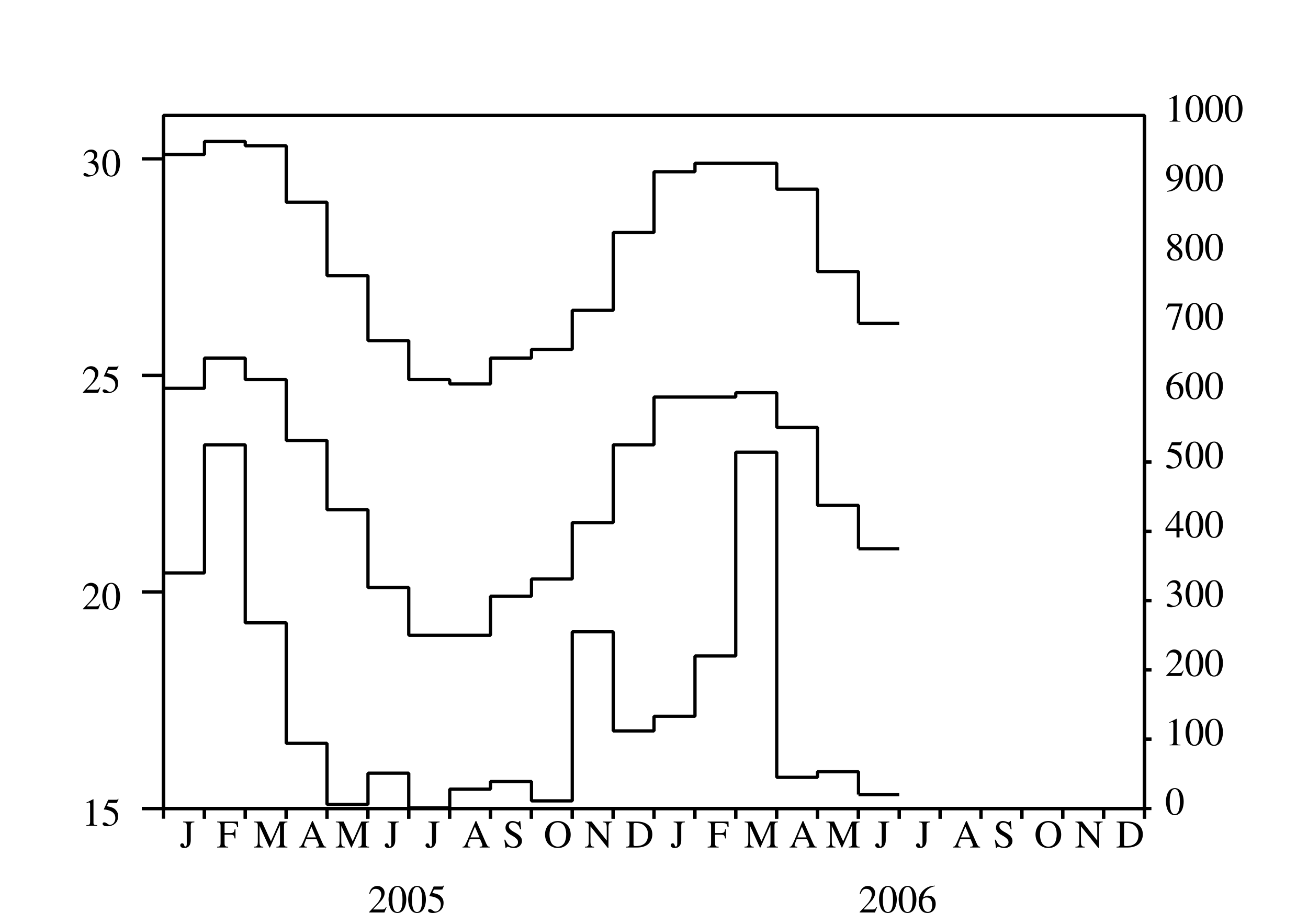
Depuis mars 2005, une épidémie de chikungunya frappe pour la première fois l'île de La Réunion, un département français d'outre-mer situé dans l'océan Indien. Après un premier pic avec plus de 400 nouveaux cas humains par semaine en mai 2005, l'épidémie a ralenti (figure 1a) à cause de l'hiver austral, qui est plus frais et moins pluvieux (figure 1b) et donc moins favorable à la prolifération d'Aedes albopictus, le moustique qui transmet le virus du chikungunya aux humains. Noter que La Réunion est dans l'hémisphère sud. Aedes albopictus a été aussi responsable d'une petite épidémie de dengue qui a duré d'avril à juillet 2004, c'est-à-dire jusqu'au début de l'hiver austral (Pierre et coll., 2005). Ceci a probablement conduit les épidémiologistes locaux à croire que le scénario de l'épidémie de dengue se répéterait avec le chikungunya ; le contrôle vectoriel de petite ampleur, associé à la recherche active de cas humains, serait suffisant pour arrêter l'épidémie avant la fin de l'hiver. Cela n'a pas été le cas. Après avoir atteint un minimum inférieur à 100 nouveaux cas par semaine en septembre 2005, l'épidémie de chikungunya a recommencé à croître et a atteint un pic étonnant de \(40\,000\) nouveaux cas par semaine en février 2006. À ce moment-là, l'épidémie était devenue un sujet de controverse scientifique et politique. Pourquoi les épidémiologistes n'avaient-ils pas été capables de prédire l'épidémie? Pourquoi le ministère de la Santé n'avait-il pas déclenché une campagne de contrôle vectoriel de grande ampleur suffisamment tôt? À présent (juillet 2006), plus de \(260\,000\) personnes ont attrapé la maladie depuis le début de l'épidémie, soit environ un tiers de la population de l'île. Environ 200 certificats de décès ont mentionné le chikungunya comme l'une des causes du décès. Par ailleurs, l'épidémie a eu un effet important sur l'économie de l'île, en particulier sur le tourisme, qui est l'une des principales industries. L'effet combiné de l'hiver et du contrôle vectoriel ont ramené à présent le nombre de nouveaux cas par semaine en dessous de mille.


Une question importante mais difficile est de savoir si l'épidémie traversera l'hiver une nouvelle fois et causera un nouveau pic important l'été prochain. Les scientifiques ont l'habitude de penser de manière simplifiée à ce genre de question. Ils s'intéressent à un paramètre clé associé avec l'épidémie, la reproductivité \(R_0\), définie de manière vague comme le nombre moyen de cas secondaires causés par un premier cas au début de l'épidémie. Si \(R_0 > 1\), alors l'épidémie se développe. Si \(R_0 < 1\), alors elle s'arrête. À la suite des travaux de Ronald Ross (1911) sur le paludisme, on a obtenu la formule suivante pour la reproductivité dans le cas des maladies à vecteurs: \begin{equation}\tag{1} R_0=\frac{\beta^2\, q\, q'\, p}{\alpha\, \mu\, P}\, , \end{equation} où \(\beta\) est la fréquence avec laquelle les vecteurs piquent, \(q\) et \(q'\) sont les probabilités de transmission par piqûre du vecteur à l'humain et de l'humain au vecteur, \(p\) est la population de vecteurs, \(P\) est la population humaine, \(1/\alpha\) est la durée d'infection moyenne chez les humains et \(1/\mu\) est l'espérance de vie des vecteurs adultes (voir (Bailey, 1982 ; Anderson et May, 1991) et (Heesterbeek, 2002) pour une perspective historique). Cette formule montre en particulier que l reproductivité est proportionnelle à la population de vecteurs. Si par conséquent un système de surveillance pouvait suivre l'évolution de la densité de vecteurs avant et pendant une épidémie, et si la valeur numérique de \(R_0\) était connue d'une épidémie précédente ou estimée avec la formule (1), alors on s'attendrait à ce que l'épidémie s'arrête lorsqu'une intervention contre les vecteurs a divisé leur densité par \(R_0\). Mais puisque qu'aucun système de surveillance ne suit actuellement la densité d'Aedes albopictus à La Réunion, la méthode que l'on vient de décrire ne peut pas marcher. Il semble donc simplement impossible de répondre raisonnablement à la question de savoir si l'épidémie de chikungunya traversera l'hiver une nouvelle fois.
Dans cet article, on se concentre sur la partie plus théorique du problème, à savoir l'estimation de la reproductivité \(R_0\). Un aspect frappant de l'épidémie de chikungunya est sa saisonnalité. Or la formule (1) suppose que la population p de vecteurs est constante tout au long de l'année. Plusieurs questions se posent: comment définir la reproductivité si l'on prend en compte la saisonnalité, par exemple si l'on suppose que la population de vecteurs est une fonction périodique du temps ? Comment calculer cette reproductivité ? Y-a-t-il des cas particuliers où l'on peut obtenir une formule simple semblable à (1)? Ces questions ne sont évidemment pas spécifiques au chikungunya. Elles se posent par exemple lors de l'émergence d'autres maladies à vecteurs et plus généralement pour les problèmes de dynamique des populations influencés par la saisonnalité : épidémiologie (Altizer et coll., 2006), écologie, démographie, immunologie, génétique des populations...
Un travail récent (Bacaër et Guernaoui, 2006) a commencé à répondre à quelques unes de ces questions. Il contient une définition de la reproductivité dans un environnement périodique comme rayon spectral d'un opérateur linéaire intégral sur un espace de fonctions périodiques. La définition est inspirée par des travaux antérieurs sur la dynamique des populations structurées par âge avec coefficients périodiques (Coale, 1972 ; Thieme, 1984 ; Jagers et Nerman, 1985 ; Anita et coll., 1998) et par le livre de Diekmann et Heesterbeek (2000), qui met en avant la notion de « matrice de prochaine génération » et d'« opérateur de prochaine génération » pour définir la reproductivité. (Bacaër et Guernaoui, 2006) contient aussi un algorithme basé sur la discrétisation de l'opérateur intégral. On a utilisé cet algorithme pour estimer la reproductivité lors d'une épidémie de leishmaniose au Maroc. On connaissait avec précision les fluctuations de la population de vecteurs grâce à des enquêtes de terrain.
Notre article s'organise de la manière suivante. Dans la section 2, on introduit une petite modification de la définition de la reproductivité donnée par (Bacaër et Guernaoui, 2006, §5). On nomme ici \(r_0\) le rayon spectral de « l'opérateur de prochaine génération », tandis que \(R_0=r_0^n\) où \(n\) est le nombre de compartiments infectés du modèle. (Heesterbeek et Roberts, 1995b, §2.1) a déjà discuté brièvement de ce point dans le cas des « matrices de prochaine génération ». On montre aussi pour une certaine classe de modèles, que l'on nomme « cycliques », que le problème intégral de valeur propre en dimension n se réduit à un problème unidimensionnel. Dans la plus grande partie de l'article, on s'intéresse au cas particulier où le noyau du problème réduit est de la forme \(K(x,t)=f(t)\, G(x)\), où \(f(t)\) est une fonction périodique. Ce cas inclut déjà de nombreux modèles de maladies à vecteurs et de maladies transmises directement.
Dans la section 3, on présente quatre méthodes numériques pour le calcul de la reproductivité dans des problèmes intégraux de valeur propre unidimensionnels. La première méthode est celle déjà présentée dans (Bacaër et Guernaoui, 2006, §4): c'est une simple discrétisation de l'opérateur intégral. La seconde méthode utilise les séries de Fourier et s'inspire de (Williams et Dye, 1997), qui étudie le paramètre malthusien et non la reproductivité . Ces deux méthodes marchent pour une fonction générale \(G(x)\) et une fonction périodique \(f(t)\). La troisième méthode ne concerne que le cas particulier où \(f(t)=1+\varepsilon \cos(\omega t - \phi)\) ; elle combine des séries de Fourier avec une méthode de perturbation pour \(\varepsilon\) petit. Elle ressemble à celle de (Coale, 1972, chapitre 6), qui s'intéresse également au paramètre malthusien et non à la reproductivité . La quatrième méthode marche pour les opérateurs de prochaine génération cycliques associés aux systèmes linéaires d'équations différentielles ordinaires à coefficients périodiques. Elle utilise la théorie de Floquet comme dans (Heesterbeek et Roberts, 1995a, 1995b) mais d'une manière différente.
Dans la section 4, on considère des maladies à vecteurs et l'on suppose que la population de vecteurs est donnée par \begin{equation}\tag{2} p(t) = p_0 \bigl [1 +\varepsilon \cos\bigl (\omega t-\phi \bigr ) \bigr ]\, . \end{equation} En utilisant tout d'abord un modèle simple pour le paludisme et les résultats de la section 3.3, on montre qu'avec les mêmes notations que dans (1), la reproductivité est donnée par \begin{equation}\tag{3} R_0 \simeq \frac{\beta^2\, q\, q' \, p_0}{\alpha\, \mu\, P} \Bigl ( 1 - \frac{\alpha \mu}{\omega^2 + (\alpha+\mu)^2}\ \frac{\varepsilon^2}{2} \Bigr ) \end{equation} où \(\varepsilon\) est petit. Cette formule apparemment nouvelle généralise la formule (1). Le premier terme est semblable au cas d'une population constante de vecteurs mais avec la population remplacé par sa moyenne. La correction relative maximale due au second terme est \(\varepsilon^2/8\) et tend toujours à diminuer la reproductivité. On se tourne ensuite vers l'épidémie de chikungunya en utilisant un modèle légèrement plus compliqué. La forme simplifiée (2) pour la population de vecteurs ne semble pas trop déraisonnable quand on regarde les courbes de température et de précipitations à La Réunion (figure 1b): les deux n'ont qu'un maximum chaque année vers février. Après avoir estimé les paramètres de ce modèle, on compare les quatre méthodes numériques de la section 3 pour le calcul de la reproductivité. Cependant on ne devrait pas trop prendre au sérieux la valeur numérique ainsi obtenue pour la reproductivité de l'épidémie de chikungunya. Les valeurs des paramètres ne sont pas connues précisément ; l'hypothèse (2) est simpliste. C'est un exercice pour tester les différentes méthodes numériques. C'est une source d'inspiration pour développer la théorie. C'est une première tentative de modélisation en attendant des études de terrain sur les fluctuations de la population de moustiques.
La dernière section discute de l'applicabilité de la méthode de la section 3.3 pour obtenir des formules approchées pour la reproductivité dans le cadre d'autres modèles mathématiques de maladies infectieuses avec coefficients périodiques, en particulier pour le modèle SIR avec un taux périodique de contacts et une période infectieuse fixe, et aussi pour le modèle SEIR avec un taux périodique de contacts et des périodes de latence et d'infectiosité distribuées exponentiellement. On présente aussi des indications préliminaires sur la signification de la reproductivité dans les modèles épidémiques stochastiques avec saisonnalité.
Pour \(t \in \mathbb{R}\) et \(x\geq 0\), on suppose que \(K(t,x)\) est une matrice de taille n à coefficients positifs ou nuls. On supposons que \(K(t+\theta,x)=K(t,x)\) si \(x\geq 0\).
L'idée derrière la fonction \(K(t,x)\) est celle d'un modèle épidémique avec \(n\) compartiments « infectés » \((I_1,I_2,\ldots,I_n)\), qui peuvent être infectieux ou latents. Le coefficient \(K_{i,j}(t,x)\) dans la ligne \(i\) et la colonne \(j\) représente l'espérance du nombre d'individus dans le compartiment \(I_i\) qu'un individu du compartiment \(I_j\) infecte au début d'une épidémie par unité de temps au temps t, s'il est dans le compartiment \(I_j\) depuis \(x\) unités de temps. Cela couvre le cas où des individus dans le compartiment \(I_j\) infectent des individus qui se retrouvent dans le compartment \(I_i\), mais aussi le cas où des individus dans le compartiment \(I_j\) changent simplement de compartiment pour se retrouver dans \(I_i\). L'hypothèse de périodicité sur \(K(t,x)\) représente un environnement périodique.
Considérons l'opérateur linéaire intégral \(\mathcal{K}\) défini par \begin{equation}\tag{4} (\mathcal{K}v)(t)=\int_0^\infty K(t,x)\, v(t-x)\, dx \end{equation} sur un espace de fonctions \(\theta\)-périodiques à valeurs dans \(\mathbb{R}^n\). Pour être plus précis, on remarque qu'avec les hypothèses de périodicité sur \(K(t,x)\) et \(v(t)\), l'équation (4) peut s'écrire \[(\mathcal{K}v)(t)=\int_0^\theta \widehat{K}(t,s)\, v(s)\, ds\] où \[\widehat{K}(t,s)=\left \{\begin{array}{ll} \sum_{k=0}^{+\infty} K(t,t-s+k\, \theta), & \quad s < t,\\ \sum_{k=1}^{+\infty} K(t,t-s+k\, \theta), & \quad s > t. \end{array} \right.\] On supposons que \(\widehat{K}\) appartient à l'espace \(L^2((0,\theta) \times (0,\theta),\mathbb{R}^{n\times n})\). Une simple extension du théorème 7 de (Hochstadt, 1973, p. 51) montre que \(\mathcal{K}\) est un opérateur linéaire compact de \(L^2( (0,\theta),\mathbb{R}^n)\) dans lui-même. Comme dans (Diekmann et Heesterbeek, 2000, p. 77), on peut nommer \(\mathcal{K}\) « l'opérateur linéaire de prochaine génération », et \(K(t,x)\) le noyau associé. Si \(r_0\) est le rayon spectral de \(\mathcal{K}\), on définit la reproductivité \(R_0\) par la formule \(R_0=r_0^n\). Voir (Heesterbeek et Roberts, 1995b, §2.1) pour une discussion de pourquoi il est parfois plus commode de prendre \(R_0=r_0^n\) que \(R_0=r_0\). Voir aussi (Bacaër et Guernaoui, 2006, §5) pour une discussion de pourquoi cette définition de \(R_0\) généralise la définition habituelle sans saisonnalité basée sur la « matrice de prochaine génération » (Diekmann et Heesterbeek, 2000, p. 74).
L'opérateur linéaire \(\mathcal{K}\) est positif. Si \(r_0 > 0\), le théorème de Krein et Rutman (voir le théorème 9.2 dans (Krasnosel'skij et coll., 1980, p. 87)) montre que \(r_0\) est une valeur propre de \(\mathcal{K}\) et qu'il existe une fonction propre positive \(v(t)\in L^2((0,\theta),\mathbb{R}^n)\) associée à \(r_0\). En étendant \(v(t)\) par périodicité à \(\mathbb{R}\), on peut écrire \begin{equation}\tag{5} \int_0^\infty K(t,x)\, v(t-x)\, dx = r_0\, v(t)\, . \end{equation} On trouve chez (Krasnosel'skij et coll., 1980) et (Schaefer, 1974, p. 377) des conditions qui assurent que \(r_0 > 0\).
Dans le reste de cet article, on considère des modèles « cycliques » qui ont la forme particulière suivante (figure 2): tous les éléments \(K_{i,j}(t,x)\) du noyau sont nuls sauf \(K_{1,n}(t,x)\) et \(K_{j+1,j}(t,x)\) pour \(1\leq j\leq n-1\).

Ceci inclut en particulier le cas général unidimensionnel \(n=1\) avec un noyau arbitraire \(K(t,x)\). Si \(v(t)=(v_1(t),\ldots,v_n(t))\), le problème intégral de valeur propre (5) s'écrit \begin{eqnarray*} \int_0^\infty K_{1,n}(t,x)\, v_n(t-x)\, dx &=& r_0\, v_1(t),\\ \int_0^\infty K_{j+1,j}(t,x)\, v_j(t-x)\, dx &=& r_0\, v_{j+1}(t),\quad 1\leq j \leq n-1. \end{eqnarray*} On remplace successivement l'équation avec \(j=n-1\), \(j=n-2\), \(\ldots\) \(j=1\) dans la première équation. Parce que \(R_0=r_0^n\), on voit que \begin{align*} \int_0^\infty\!\!\!\!\!\cdots \int_0^\infty &K_{1,n}(t,x_1)\, K_{n,n-1}(t-x_1,x_2) \cdots\, K_{2,1}(t-x_1-\cdots-x_{n-1},x_n)\\ &v_1(t-x_1-\cdots - x_n)\, dx_1\cdots dx_n = R_0\, v_1(t). \end{align*} Il faut noter une propriété importante: si un élément non nul \(K_{i,j}(t,x)\) est multiplié par une certaine constante, alors \(R_0\) est aussi multiplié par la même constante. Le changement de variable \((x_1=x_1,\ldots,x_{n-1}=x_{n-1},x=x_1+\cdots+x_n)\) conduit à \begin{equation}\tag{6} \int_0^\infty \widetilde{K}(t,x)\, v_1(t-x)\, dx = R_0\, v_1(t), \end{equation} où \(\widetilde{K}(t,x)\) est l'intégrale d'hypersurface \[\widetilde{K}(t,x) = \int_{\sigma_x^n} \!\!\!K_{1,n}(t,x_1)\, K_{n,n-1}(t-x_1,x_2) \cdots\, K_{2,1}(t-x_1-\cdots-x_{n-1},x_n)\, d\sigma_x^n\] et \(\sigma_x^n=\{(x_1,\ldots,x_n) \in \mathbb{R}^n; x_1+\cdots+x_n = x, x_1\geq 0, \ldots, x_n \geq 0\}\). Ainsi on a réduit le problème intégral \(n\)-dimensionnel de valeur propre (5) à un problème unidimensionnel (6).
Dans le reste de l'article sauf dans la section 3.4, on considère le cas particulier où \begin{equation}\tag{7} K_{1,n}(t,x)=f(t)\, g_n(x),\quad K_{j+1,j}(t,x)=g_j(x),\ 1\leq j\leq n-1. \end{equation} L'équation (6) devient \begin{equation}\tag{8} f(t) \int_0^\infty G(x)\, v_1(t-x)\, dx = R_0\, v_1(t), \end{equation} où \begin{equation}\tag{9} G(x)=\int_{\sigma_x^n} g_1(x_1) \cdots g_n(x_n)\, d\sigma_x. \end{equation} Noter que si \(n=1\), le noyau se réduit à \(K(t,x)=f(t)\, g_1(x)\) de sorte que \(G(x)=g_1(x)\). Noter aussi que si \begin{equation}\tag{10} g_j(x)=a_j\, e^{-b_j\, x}, \quad 1\leq j\leq n, \end{equation} on peut montrer (voir appendice) en partant de (9) que \begin{equation}\tag{11} G(x)=a_1 \cdots a_n \sum_{j=1}^n \frac{e^{-b_j\, x}}{\prod_{k\neq j} (b_k-b_j)}\, . \end{equation} Cette formula reste valable pour \(n=1\) avec la convention usuelle que le produit sur un ensemble vide est égal à 1.
Cette méthode consiste à discrétiser le problème intégral de valeur propre (8). Elle est présentée dans (Bacaër et Guernaoui, 2006, §4); on ne la rappelle donc que brièvement. On prend un entier N très grand et \(t_k=(k-1)\, \theta /N\), où \(k=1,2,\ldots,N\). On définit \begin{equation}\tag{12} \widehat{G}(x)=\sum_{k=0}^{+\infty} G(x+k\, \theta). \end{equation} On nomme \(\mathcal{R}_0\) le rayon spectral de la matrice du problème de valeur propre \begin{equation}\tag{13} f(t_k)\, \frac{\theta}{N} \Bigl [\sum_{j=1}^{k-1} \widehat{G}(t_k-t_j)\, \mathcal{V}_j + \sum_{j=k}^{N} \widehat{G}(t_k-t_j+\theta)\, \mathcal{V}_j \Bigr ] = \mathcal{R}_0\, \mathcal{V}_k\ , \end{equation} où \(\mathcal{V}_i\) est un vecteur propre. Alors \(\mathcal{R}_0\to R_0\) si \(N\to +\infty\). Le calcul numérique de \(\mathcal{R}_0\) peut se faire avec Scilab (www.scilab.org), un logiciel libre semblable à Matlab. Noter que si \(g_j(x)=a_j\, e^{-b_j\, x}\) pour tout \(1\leq j\leq n\), il résulte de (11) que \begin{equation}\tag{14} \widehat{G}(x)=a_1 \cdots a_n \sum_{j=1}^n \frac{e^{-b_j\, x}}{(1-e^{-b_j\, \theta})\, \prod_{i\neq j} (b_i-b_j)}\, . \end{equation}
Si \(\omega=2\pi/\theta\), considérons la décomposition de Fourier de la fonction périodique \(f(t)\) : \begin{equation}\tag{15} f(t)=\sum_{j\in \mathbb{Z}} f_j\, e^{j i \omega t},\quad f_j=\frac{1}{\theta} \int_0^\theta f(t)\, e^{-j i \omega t}\, dt\, , \end{equation} où \(\mathbb{Z}\) est l'ensemble des entiers (positifs ou négatifs) et \(i^2=-1\). Les \(f_j\) sont des nombres complexes avec \(f_{-j}=f_j^*\) (\(^*\) désigne le nombre complexe conjugué). On cherche une solution de (8) qui est une fonction réelle (et même positive) de la forme \begin{equation}\tag{16} v_1(t)=\sum_{j \in \mathbb{Z}} c_j\, e^{j i \omega t}. \end{equation} Les \(c_j\) sont aussi des nombres complexes avec \(c_{-j}=c_j^*\). On remplace (15) et (16) dans (8): \begin{equation}\tag{17} \Bigl (\sum_{j \in \mathbb{Z}} f_j\, e^{j i\omega t}\Bigr ) \Bigl ( \sum_{j \in \mathbb{Z}} G_j \, c_j \, e^{j i \omega t} \Bigr )= R_0 \sum_{j \in \mathbb{Z}} c_j\, e^{j i \omega t}\, , \end{equation} où \begin{equation}\tag{18} G_j=\int_0^\infty G(x)\, e^{- j i \omega x}\, dx\, . \end{equation} Il résulte de (9) que \begin{equation}\tag{19} G_j= \Bigl (\int_0^\infty g_1(x)\, e^{-j i \omega x}\, dx \Bigr ) \cdots \Bigl (\int_0^\infty g_n(x)\, e^{-j i \omega x}\, dx \Bigr ). \end{equation} Si \(g_j(x)=a_j\, e^{-b_j\, x}\) pour \(1\leq j\leq n\), alors \begin{equation}\tag{20} G_j = \frac{a_1 \cdots a_n}{(b_1+j i \omega) \cdots (b_n + j i \omega)} \end{equation} pour \(j\in \mathbb{Z}\). L'équation (17) peut s'écrire \[ \sum_{j \in \mathbb{Z}} \Bigl ( \sum_{k \in \mathbb{Z}} f_{j-k}\, G_k\, c_k \Bigr ) e^{j i \omega t} = R_0 \sum_{j \in \mathbb{Z}} c_j\, e^{j i \omega t} .\] Cette égalité est vraie si et seulement si \begin{equation}\tag{21} \sum_{k \in \mathbb{Z}} f_{j-k}\, G_k\, c_k = R_0\, c_j \end{equation} pour \(j\in \mathbb{Z}\). C'est un problème de valeur propre pour une matrice infinie. Noter que \(f_k \to 0\) et \(G_k \to 0\) si \(k \to \pm \infty\). Donc si on laisse N grandir et si \(\mathcal{R}_0\) est le rayon spectral de la matrice carrée tronquée \((f_{j-k}\, G_k)_{-N\leq j,k \leq N}\), alors \(\mathcal{R}_0\to R_0\) si \(N\to +\infty\).
On suppose que \begin{equation}\tag{22} f(t)=1+\varepsilon \cos \bigl (\omega t-\phi \bigr ), \end{equation} où \(0\leq \varepsilon \leq 1\) et \(0\leq \phi < 2\pi\). C'est ce que l'on appelle une fonction « sinusoïdale ». Pour le problème de valeur propre (8), un décalage dans le temps de \(f(t)\) ne change pas \(R_0\). En effet, si \(R_0\) est le rayon spectral associé à \(f(t)\) avec la fonction propre \(v_1(t)\), alors \(R_0\) est encore le rayon spectral associé à \(\hat{f}(t)=f(t-h)\) avec la fonction propre \(\hat{v}_1(t)=v_1(t-h)\). Pour le calcul de \(R_0\), on peut donc supposer que \(\phi=0\), de sorte que \[ f(t)=1 + \frac{\varepsilon}{2}\, e^{i\omega t} + \frac{\varepsilon}{2}\, e^{-i\omega t}. \] De manière évidente, on a \(f_0=1\), \(f_1=f_{-1}=\frac{\varepsilon}{2}\) et \(f_k=0\) pour \(|k| > 1\). Le système (21) devient \begin{equation}\tag{23} \frac{\varepsilon}{2} \, G_{j-1}\, c_{j-1} + G_j\, c_j + \frac{\varepsilon}{2}\, G_{j+1}\, c_{j+1} = R_0\, c_j \end{equation} pour \(j\in \mathbb{Z}\). Parce que \(G(x)\) est à valeurs réelles, on a \(G_{-j}=G_j^*\). De ce fait, il résulte que l'équation (23) avec \(c_{-j}\) dans le côté droit est simplement le complexe conjugué de l'équation (23) avec \(c_j\) dans le côté droit. On peut donc oublier l'équation (23) pour \(j < 0\). Rappelons que \(c_{-1}=c_1^*\) et \(G_{-1}=G_1^*\). Le problème de valeur propre (23) avec \(j\in \mathbb{Z}\) se réduit à \begin{equation}\left \{\begin{array}{ccccccl} \frac{\varepsilon}{2}\, G_1^*\, c_1^* &+& G_0\, c_0 &+& \frac{\varepsilon}{2}\, G_1\, c_1 &= &R_0 \, c_0\, ,\\ \frac{\varepsilon}{2}\, G_{j-1}\, c_{j-1} &+& G_j\, c_j &+& \frac{\varepsilon}{2}\, G_{j+1}\, c_{j+1} &=& R_0\, c_j\, ,\ (j\geq 1). \end{array}\right. \tag{24} \end{equation} La fonction propre \(v_1(t)\) peut être normalisée de sorte que \(c_0=1\). C'est possible parce que \(v_1(t)\) est strictement positif de sorte que \(c_0=\frac{1}{\theta} \int_0^\theta v_1(t)\, dt > 0\). Cherchons une solution du système (24) de la forme \begin{equation}\tag{25} R_0=\sum_{k\geq 0} \rho_{k}\, \varepsilon^k,\quad c_j=\sum_{k\geq 0} c_{j,k}\, \varepsilon^k, \end{equation} dont on attend qu'elle soit valable au moins pour \(\varepsilon\) petit. Avec \(c_0=1\), noter que \(c_{0,0}=1\) et \(c_{0,k}=0\) pour tout \(k\geq 1\). On insère (25) dans la première équation de (24) et l'on sépare les puissances de \(\varepsilon^k\). On obtient \(G_0 = \rho_{0}\) et \begin{equation}\tag{26} \frac{G_1^*}{2}\, c_{1,k-1}^* + \frac{G_1}{2}\, c_{1,k-1} = \rho_{k} \end{equation} pour \(k\geq 1\). De même, en insérant (25) dans la seconde équation de (24), on arrive à \(G_j\, c_{j,0} = \rho_{0}\, c_{j,0}\) pour \(j\geq 1\) et \begin{equation}\tag{27} \frac{G_{j-1}}{2}\, c_{j-1,k-1} + G_j\, c_{j,k} + \frac{G_{j+1}}{2}\, c_{j+1,k-1} = \sum_{l=0}^k \rho_{l}\, c_{j,k-l} \end{equation} pour \(j\geq 1\) et \(k\geq 1\). Pour \(j\geq 1\), il résulte que \((G_0-G_j)\, c_{j,0} =0\). Donc \(c_{j,0}=0\) parce que \(G(x)\) est positif et non identiquement nul de sorte que \(G_0-G_j=\int_0^\infty (1-e^{-ji\omega x})\, G(x)\, dx\neq 0\). Parce que \[\rho_{0}= G_0,\quad c_{j,0}=0\ (j\geq 1),\quad c_{0,0}=1,\quad c_{0,k}=0\ (k\geq 1),\] on voit avec (26) et (27) que les coefficients \(\rho_{k}\) et \(c_{j,k}\) pour \(j\geq 1\) et \(k\geq 1\) se calculent récursivement: \begin{eqnarray} \rho_{k} &=& \Re ( G_1\, c_{1,k-1})\, ,\tag{28}\\ c_{j,k} &=& \frac{1}{G_0-G_j} \Bigl [ \frac{G_{j-1}}{2}\, c_{j-1,k-1} + \frac{G_{j+1}}{2}\, c_{j+1,k-1} - \sum_{l=1}^{k-1} \rho_{l}\, c_{j,k-l} \Bigr ],\tag{29} \end{eqnarray} où \(\Re(z)\) désigne la partie réelle du nombre complexe \(z\). Plus précisément, si les coefficients \(\rho_l\) et \(c_{j,l}\) sont calculés pour \(l\leq k-1\) et \(j\geq 1\), alors les formules donnent une expression pour \(\rho_k\) et \(c_{j,k}\) pour \(j\geq 1\). Cet algorithme peut démarrer parce que \(\rho_0\) et les coefficients \(c_{j,0}\) sont connus. En utilisant (28)-(29), on voit facilement que \(c_{j,k}=0\) pour \(j > k\), que \(\rho_k=0\) pour tout entier impair \(k\), et que \(c_{j,k}=0\) si \(j\geq 1\) est impair alors que \(k\geq 1\) est pair.
En pratique, fixons un entier \(\kappa > 1\) et considérons le vecteur \((\rho_k)_{0\leq k\leq \kappa}\) et la matrice rectangulaire \((c_{j,k})_{0\leq j\leq \kappa+1,\, 0\leq k\leq \kappa}\). Fixons \(\rho_0= G_0\), \(c_{0,0}=1\), \(c_{j,k}=0\) pour \(j > k\) dans la matrice, et \(c_{0,k}=0\) pour \(1\leq k\leq \kappa\). L'algorithme fonctionne ainsi:
| pour \(k\)=1 à \(\kappa\), |
| calculer \(\rho_k\) en utilisant (28) |
| pour \(j\)=1 à \(k\), |
| calculer \(c_{j,k}\) en utilisant (29) |
| fin; |
| fin. |
De cette manière, on voit facilement que \begin{equation}\tag{30} \rho_1=0,\quad c_{1,1}=\frac{G_0}{2(G_0-G_1)},\quad \rho_2=\frac{1}{2}\, \Re \Bigl (\frac{G_0\, G_1}{G_0-G_1} \Bigr ), \end{equation} Finalement on trouve \begin{equation}\tag{31} R_0 \simeq G_0 + \frac{\varepsilon^2}{2}\, \Re \Bigl (\frac{G_0\, G_1}{G_0-G_1} \Bigr ) \end{equation} pour \(\varepsilon\) petit; c'est la correction d'ordre le plus bas à la reproductivité lorsque des variations saisonnières de petite amplitude sont prises en compte. Faisons quelques remarques additionnelles:
Dans cette section, on considère le système linéaire d'équations différentielles ordinaires \begin{align} \frac{dI_1}{dt} &= -\alpha_1(t)\, I_1(t) + \beta_n(t)\, I_n(t),\tag{32}\\ \frac{dI_{j+1}}{dt} &= -\alpha_{j+1}(t)\, I_{j+1}(t)+ \beta_{j}\, I_{j}(t),\quad 1\leq j\leq n-1, \tag{33} \end{align} où toutes les fonctions \(\alpha_j(t)\) et \(\beta_j(t)\) sont \(\theta\)-périodiques. Ce système peut venir de la linéarisation près de l'équilibre sans maladie d'un modèle épidémique non linéaire. Le noyau de l'opérateur de prochaine génération associé est donné par \begin{align*} K_{1,n}(t,x)&=\beta_n(t)\, e^{-\int_{t-x}^t \alpha_n(s)\, ds},\\ K_{j+1,j}(x,t)&=\beta_j(t)\, e^{-\int_{t-x}^t \alpha_{j+1}(s)\, dx},\quad 1\leq j \leq n-1, \end{align*} et \(K_{i,j}(t,x)=0\) pour tous les autres indices. C'est donc un modèle « cyclique » au sens de la section 2. Une remarque dans cette section montre que si par exemple \(\beta_n(t)\) est multiplié par une certaine constante, alors la reproductivité est multiplié par la même constante.
La théorie de Floquet appliquée au système (32)-(33) montre que l'équilibre nul est instable si et seulement si le rayon spectral de la « matrice de prochaine année », aussi appelée matrice de monodromie, est supérieur à 1. Donc la reproductivité est aussi l'unique nombre réel positif, pour lequel \(\rho(X(\theta))=1\), où \(\rho\) est le rayon spectral de la matrice et \[\frac{dX}{dt}(t)=\left (\begin{array}{ccccc} -\alpha_1(t) & 0 & \cdots & 0 & \frac{\beta_n(t)}{R_0} \\ \beta_1(t) & \ddots & \ddots & & 0\\ 0 & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & \beta_{n-1}(t) & -\alpha_n(t) \end{array}\right ) X(t)\] avec la condition initiale \(X(0)=1_n\) (la matrice identité de taille n). Ainsi \(R_0\) se calcule en combinant une méthode de dichotomie avec un logiciel résolvant numériquement les équations différentielles ordinaires tel que Scilab.
On considère dans cette section un modèle très simple pour le paludisme, à savoir une variation sur l'un des premiers modèles proposés par Ronald Ross (1911) avec une population de vecteurs périodiques. Introduisons les notations suivantes: \(S(t)\) est la population humaine saine, \(I(t)\) la population humaine infectée, \(P=S(t)+I(t)\) la population humaine totale. De même, \(s(t)\) est la population vectorielle saine, \(i(t)\) la population vectorielle infectée et \(p(t)=s(t)+i(t)\) la population vectorielle totale. Par ailleurs, on considère les paramètres suivants: \(\alpha\) est la vitesse de guérison des humains; \(\beta\) est la fréquence à laquelle les vecteurs piquent; \(q\) (ou \(q'\)) est la probabilité de transmission par piqûre du vecteur à l'humain (ou de l'humain au vecteur); \(\lambda(t)\) est le nombre de nouveaux vecteurs adultes qui émergent par unité de temps, qui est une fonction \(\theta\)-périodique; \(\mu\) est la mortalité des vecteurs. Le modèle est le suivant: \begin{align} \frac{ds}{dt}&= \lambda(t) - \beta\, q'\, s(t)\, \frac{I(t)}{P} - \mu\, s(t),\tag{34}\\ \frac{di}{dt} &= \beta\, q'\, s(t)\, \frac{I(t)}{P} -\mu\, i(t) ,\tag{35}\\ \frac{dS}{dt} &= -\beta\, q\, i(t)\, \frac{S(t)}{P} + \alpha\, I(t)\, ,\tag{36}\\ \frac{dI}{dt} &= \beta\, q\, i(t)\, \frac{S(t)}{P} -\alpha\, I(t)\, .\tag{37} \end{align} En additionnant (34) et (35), on voit que \(\frac{dp}{dt}=\lambda(t) -\mu\, p(t)\). On suppose que \(p(t)\) est donné par \[p(t)=p_0 [1+\varepsilon \cos (\omega t - \phi)].\] Comme \(\mu\) est connu, ceci détermine \(\lambda(t)\). En linéarisant le système (34)-(37) près de l'équilibre sans maladie, on obtient \begin{equation}\tag{38} \frac{di_*}{dt} = \beta\, q'\, p(t)\, \frac{I_*(t)}{P} -\mu\, i_*(t)\, ,\quad \frac{dI_*}{dt} = \beta\, q\, i_*(t) -\alpha\, I_*(t)\, . \end{equation} Le noyau de l'opérateur de prochaine génération associé est \begin{equation}\tag{39} K(t,x)=\left (\begin{array}{cc} 0 & \frac{\beta\, q'\, p(t)}{P}\, e^{-\alpha\, x}\\ \beta\, q\, e^{-\mu\, x} & 0 \end{array}\right )\, . \end{equation} Il est « cyclique » de la forme particulière (7), avec les fonctions \(g_j(x)\) (\(1\leq j\leq 2\)) de la forme (10) et \(f(t)=1+\varepsilon \cos (\omega t - \phi)\). La formule (20) donne \begin{equation}\tag{40} G_j=\frac{\beta^2\, q\, q'\, p_0}{(\alpha+j i \omega) (\mu + j i \omega) P} \end{equation} pour \(j \in \mathbb{Z}\). Finalement (31) est de la forme \begin{equation} R_0 \simeq \frac{\beta^2\, q\, q' \, p_0}{\alpha\, \mu\, P} \Bigl ( 1 - \frac{\alpha \mu}{\omega^2 + (\alpha+\mu)^2} \ \frac{\varepsilon^2}{2} \Bigr ) ,\tag{41} \end{equation} C'est la correction d'ordre le plus bas à la formule (1). Noter qu'on a l'inégalité \[0\leq \frac{\alpha \mu}{\omega^2 + (\alpha+\mu)^2}\ \frac{\varepsilon^2}{2} \leq \frac{\varepsilon^2}{8}\, .\] La borne supérieure est atteinte lorsque \(\alpha \simeq \mu \gg \omega\). Ainsi on arrive à la conclusion suivante:
Le premier terme dans la formule pour \(R_0\) est le même que pour le cas d'une population \(p\) constante de vecteurs mais avec \(p\) remplacé par la population vectorielle moyenne \(p_0\). La correction relative maximale due au second terme est \(\varepsilon^2/8\) et tend toujours à diminuer \(R_0\). Donc il est légèrement plus difficile pour une maladie à vecteurs d'envahir une population avec des fluctuations.On rappelle aussi deux propriétés fondamentales de \(R_0\) dans le contexte des maladies à vecteurs: une épidémie peut se développer si et seulement si \(R_0 > 1\) ; une épidémie peut être évitée si la population \(p(t)\) de vecteurs est uniformément divisée par \(R_0\) tout au long de l'année.
La chikungunya est une maladie virale qui semble conduire à une immunité durable. Si de plus on veut prendre en compte la période d'incubation chez les humains et les vecteurs, le modèle suivant semble convenir: \begin{align} \frac{ds}{dt}&= \lambda(t) - \beta\, s(t)\, \frac{I(t)}{P} - \mu\, s(t),\tag{42}\\ \frac{de}{dt} &= \beta\, s(t)\, \frac{I(t)}{P} - (\gamma + \mu)\, e(t),\quad \frac{di}{dt} = \gamma\, e(t) -\mu\, i(t) ,\tag{43}\\ \frac{dS}{dt} &= -\beta\, i(t)\, \frac{S(t)}{P} \, ,\\ \frac{dE}{dt} &= \beta\, i(t)\, \frac{S(t)}{P} - \delta\, E(t)\, ,\quad \frac{dI}{dt} = \delta\, E(t) -\alpha\, I(t)\, ,\tag{44}\\ \frac{dR}{dt} &= \alpha\, I(t)\, ,\tag{45} \end{align} où \(e(t)\) (respectivement \(E(t)\)) est la population de vecteurs infectés mais non infectieux (respectivement humains), \(1/\gamma\) (respectivement \(1/\delta\)) est la période d'incubation moyenne chez les vecteurs (respectivement les humains) et \(R(t)\) est la population humaine immune. Noter que les probabilités de transmission dans les compartiments \(e\) et \(E\) sont nulles et celles dans les compartiments \(i\) et \(I\) égales à 1. La population humaine totale \(P=S(t)+E(t)+I(t)+R(t)\) est constante, tandis que la population vectorielle totale \(p(t)=s(t)+e(t)+i(t)\) est solution de \(\frac{dp}{dt}=\lambda(t) - \mu\, p(t)\).
On utilise ce modèle pour essayer d'estimer la reproductivité pour l'épidémie de chikungunya de 2005 et 2006 à La Réunion. Comme les fluctuations de la population de vecteurs sont inconnues, on prend la forme simple \(p(t)=p_0 (1+\varepsilon\, \cos(\omega t - \phi))\), qui n'est pas trop déraisonnable quand on observe les courbes de température et de précipitations à La Réunion (figure 1b), les deux ayant un seul maximum annuel vers février et un minimum vers juillet. Ainsi la période \(\theta=\frac{2\pi}{\omega}\) est d'un an et l'on peut prendre \(\phi=\frac{2\pi}{12}\). La fonction \(s(t)\) peut être éliminée du système (42)-(45) puisque \(s(t)=p(t)-e(t)-i(t)\). Les autres valeurs des paramètres utilisées pour la simulation sont résumées dans le tableau 1. Noter par exemple que (chikungunya.net, #83) réfère à la question 83 dans la liste des questions souvent posées du site chikungunya.net, un site mis en place par des épidémiologistes dédié à l'épidémie de chikungunya à La Réunion.
On estime que l'incubation chez les humains dure entre 3 et 7 jours (Duhamel et coll., 2006, p. 6) ou entre 4 et 7 jours (chikungunya.net, #101). Mais d'après (#156), les humains peuvent commencer à être infectieux 2 ou 3 jours avant les symptômes. On a donc choisi 4 jours pour la période d'incubation. On estime que la période infectieuse après les symptômes chez les humains est d'environ 5 jours (Duhamel et coll., 2006, p. 7) ou entre 5 et 7 jours (#49,52). Vue la remarque précédente, on prend une valeur de 7 jours pour toute la période infectieuse.
On estime que la période d'incubation chez les vecteurs est comprise entre 9 et 14 jours (chikungunya.net, #83), entre 4 et 5 jours (#253), ou entre une et deux semaines (#395). On a choisi 7 jours. Une fois infectés, il semblerait que les vecteurs le restent jusqu'à ce qu'ils meurent (#83). On estime que la durée de vie d'un vecteur adulte est comprise entre 4 et 10 semaines (#83) ou « plusieurs » semaines (#404). On a choisi un mois. Le vecteur peut piquer 5 ou 6 fois pendant sa vie (#404): on a choisi une moyenne d'une piqûre tous les 4 jours. On ignore si le vecteur infecté peut transmettre le virus à ses œufs (#83/385/442) : notre modèle ne prend pas en considération cette possibilité.
L'infection chez les humains conduit à un état d'immunité (#10/385), qui dure probablement au moins plusieurs années puisque personne ne semble avoir souffert deux fois du chikungunya durant l'épidémie à La Réunion. Les cas asymptomatiques représentent entre 10 et 15% des cas d'après (#385) mais ne semblent pas inclus dans l'estimation du nombre de cas dans la figure 1; on n'en tient pas compte dans le modèle.
| paramètre | symbole | valeur | |||
|---|---|---|---|---|---|
| période d'incubation chez les vecteurs | \(1/\gamma\) | 7 jours | |||
| durée de vie des vecteurs | \(1/\mu\) | 1 mois | |||
| période d'incubation chez les humains | \(1/\delta\) | 4 jours | |||
| période infectieuse chez les humains | \(1/\alpha\) | 7 jours | |||
| période entre deux piqûres | \(1/\beta\) | 4 jours | |||
| population de La Réunion | \(P\) | \(785\,000\) | |||
| décalage de saisonnalité | \(\phi\) | \(\frac{2\pi}{12}\) |
| \(N\) | 12 | 25 | 50 | 100 | 200 |
| \(R_0\) | \(\mbox{3,100}\) | \(\mbox{3,399}\) | \(\mbox{3,392}\) | \(\mbox{3,389}\) | \(\mbox{3,389}\) |
| \(N\) | 0 | 1 | 2 | 3 | 4 |
| \(R_0\) | \(\mbox{3,868}\) | \(\mbox{3,496}\) | \(\mbox{3,418}\) | \(\mbox{3,389}\) | \(\mbox{3,389}\) |
| \(\kappa\) | 0 | 2 | 4 | 10 | 12 |
| \(R_0\) | \(\mbox{3,868}\) | \(\mbox{3,461}\) | \(\mbox{3,409}\) | \(\mbox{3,390}\) | \(\mbox{3,389}\) |
Répétons: la valeur numérique obtenue pour \(R_0\) pour l'épidémie de chikungunya ne doit pas être prise trop au sérieux vu que les valeurs des paramètres sont imprécises et vu la simplicité de l'hypothèse (2). On peut voir cela comme un exercice pour tester les différentes méthodes numériques, comme une source d'inspiration pour développer la théorie, ou comme une première tentative de modélisation en attendant des enquêtes de terrain concernant les fluctuations de la population d'Aedes albopictus.
Considérons un modèle épidémique avec un compartiment infecté et un noyau de la forme \begin{equation}\tag{46} K(t,x)=[1+\varepsilon\, \cos(\omega t-\phi)]\, g(x). \end{equation} Alors \(G(x)=g(x)\) comme déjà noté dans la section 2 et \(R_0\) peut être approché par la formule (31). Le noyau (46) apparaît par exemple dans les modèles épidémiques SIS/SIR/SIRS avec un taux de contact sinusoïdal.
Si la période infectieuse est distribuée exponentiellement comme dans (Dietz, 1976 ; Grossman et coll., 1977 ; Kuznetsov et Piccardi, 1994), alors \(G(x)=a\, e^{-b x}\) et l'on vérifie facilement que \(G_0=a/b\) et que le coefficient de \(\varepsilon^2\) dans (31) s'annule, de sorte que \(R_0\simeq a/b\). Avec la même définition de \(R_0\) que celle de l'article présent, (Bacaër et Guernaoui, 2006, §5) a montré la formule exacte \(R_0=a/b\) dans ce cas. Bien sûr ce « résultat » a déjà été remarqué depuis longtemps, puisque le noyau (46) apparaît en connexion avec l'équation \[\frac{dI}{dt} = a (1+\varepsilon\, \cos(\omega t-\phi))\, I(t) - b\, I(t),\] que l'on peut résoudre explicitement, et pour laquelle on montre facilement que l'état d'équilibre nul est instable si et seulement si \(a/b > 1\). Par analogie avec le cas trivial où \(\varepsilon=0\), plusieurs auteurs ont posé \(R_0=a/b\) comme définition, ont remarqué que \(R_0\) était la moyenne temporelle de la fonction \(\mathcal{R}_0(t)= a (1+\varepsilon\, \cos(\omega t-\phi))/b\), et ont cru que cette propriété de moyennisation restait valable pour des modèles plus compliqués; ce n'est pas le cas.
Si la période infectieuse est une constante \(\tau\) fixée comme dans (Cooke et Kaplan, 1976 ; Smith, 1977 ; Nussbaum, 1977 ; Nussbaum, 1978 ; Grossman, 1980), alors \(G(x)=a\) pour \(x < \tau\) et \(G(x)=0\) pour \(x > \tau\). Alors \(G_0=a\, \tau\), \(G_1=a \, \frac{1-e^{-i\omega \tau}}{i\omega}\), et (31) donne \begin{equation}\tag{47} R_0\simeq a\, \tau + \varepsilon^2\, \frac{2\, a\, \tau\, \sin^2(\omega \tau/2)}{[\omega \tau - \sin(\omega \tau)]^2 + [1-\cos(\omega \tau)]^2 } \Bigl [\frac{\omega \tau/2}{\tan(\omega \tau/2)}-1 \Bigr ] \, . \end{equation} Cette formule montre que, contrairement au cas du modèle pour le paludisme de la section 4.1, la saisonnalité peut soit augmenter soit diminuer \(R_0\), suivant la valeur numérique de \(\omega \tau\). Noter que pour le cas exceptionnel où \(\omega=2\pi\) et \(a=1\) considéré par (Cooke et Kaplan, 1976 ; Smith, 1977 ; Nussbaum, 1977 ; Nussbaum, 1978), la formule (47) dit que \(R_0=1+o(\varepsilon^2)\) lorsque \(\tau=1\). On s'attend à avoir la formule exacte \(R_0=1\) pour tout \(\varepsilon\) quand \(\tau=1\), puisque (Smith, 1977 ; Nussbaum, 1977) ont montré que des solutions périodiques du modèle épidémique non linéaire complet existent si et seulement si \(\tau > 1\) .
Considérons un modèle épidémique avec deux compartiments infectés qui, une fois linéarisé près de l'équilibre sans maladie, prend la forme \[\frac{dI_1}{dt}\simeq -b_1\, I_1(t) + a_2\, [1+\varepsilon\, \cos (\omega t - \phi)]\, I_2(t),\quad \frac{dI_2}{dt} \simeq a_1\, I_1(t) - b_2\, I_2(t).\] Remarquer que le système (38) était de cette forme. Le noyau de l'opérateur de prochaine génération associé est \begin{equation}\tag{48} K(t,x)=\left (\begin{array}{cc} 0 & [1+\varepsilon\, \cos(\omega t-\phi)]\, a_2\, e^{-b_2\, x}\\ a_1\, e^{-b_1 x} & 0 \end{array}\right ). \end{equation} La formule (31) donne \begin{equation}\tag{49} R_0 \simeq \frac{a_1\, a_2}{b_1\, b_2} \Bigl (1 - \frac{b_1\, b_2}{\omega^2 + (b_1+b_2)^2} \, \frac{\varepsilon^2}{2} \Bigr )\, . \end{equation}
Un exemple de ce type est le modèle pour le paludisme de (Anderson et May, 1991, p. 404). Les valeurs numériques utilisées dans cette référence sont: \(\omega=2\pi\), \(\varepsilon=15/25\), \(a_1=20\) par année, \(a_2=20\times 25\) par année, \(b_1=50\) par année et \(b_2=4\) par année. Les quatre méthodes numériques de la section 3, de même que la formule approchée (49), donnent \(R_0\simeq \mbox{49,4}\). Noter que le terme d'ordre le plus bas est \(\rho_0=50\).
Un autre exemple est le modèle épidémique SEIR ou SEIRS avec un taux de contact sinusoïdal considéré par exemple dans (Schwartz et Smith, 1983 ; Aron et Schwartz, 1984 ; Kuznetsov et Piccardi, 1994), (Altizer et coll., 2006, encadré 1) et (Ma et Ma, 2006, §4). Les valeurs numériques utilisées par (Ma et Ma, 2006, §4) sont: \(\omega=1\), \(\varepsilon=\mbox{0,8}\), \(a_1=\mbox{0,3}\) \(a_2=1\), \(b_1=\mbox{0,3}\), et \(b_2=\mbox{0,99}\) (unités non spécifiées). Une simulation numérique a montré qu'aucune épidémie de peut s'établir dans ce cas. Mais avec \(\varepsilon=0\), les auteurs ont remarqué que \(R_0=\rho_0=(a_1\, a_2)/(b_1\, b_2)=1/\mbox{0,99} > 1\). La conclusion était que la moyennisation du taux de contact n'est pas la manière correcte de déterminer le seuil épidémique. En effet, les quatre méthodes numériques de la section 3 donnent \(R_0\simeq \mbox{0,973} < 1\) pour \(\varepsilon=\mbox{0,8}\). La formule approchée (49) donne \(R_0\simeq \mbox{0,974}\).
Un autre exemple est le modèle pour le choléra avec un taux de contact sinusoïdal avec l'eau ou un taux de contamination sinusoïdal de l'eau (Codeço, 2001). Cette référence considère aussi le cas où le coefficient \(b_2\) représentant le taux de disparition de Vibrio cholerae dans l'eau est une fonction sinusoïdale du temps. Le présent article ne fournit pas de formule approchée pour la reproductivité dans ce dernier cas, mais \(R_0\) peut toujours être calculé numériquement en utilisant par exemple la méthode de la section 3.4.
On mentionne aussi la « conjecture » de (Moneim et Greenhalgh, 2005), qui suggère que la reproductivité (avec un seuil à 1) pour un modèle SEIRS avec une vaccination et un taux de contact périodiques se calcule par une formule simple après avoir pris la moyenne des coefficients du système linéarisé sur une période. Cette référence de donne pas d'exemple numérique. Mais si l'on suppose que le taux de contact est constant et que le taux de vaccination est tel que la population susceptible dans la situation sans maladie soit sinusoïdale, alors \(K(t,x)\) est exactement de la forme (48) et \(R_0\) est donné par (49). Si la moyennisation était correcte, le résultat ne devrait pas dépendre de \(\varepsilon\). Donc la « conjecture » semble fausse.
Il serait utile pour l'épidémie de chikungunya à La Réunion d'avoir une estimation de la probabilité que l'épidémie s'éteigne à cause de l'hiver sachant la taille de la population humaine infectée au début de l'hiver. Pour répondre à cette question, on a évidemment besoin d'un modèle stochastique. Mais les modèles stochastiques pour les maladies à vecteurs avec saisonnalité sont difficiles à analyser. Dans cette section, on montre le lien qui existe entre la probabilité d'extinction au temps \(t\) et la reproductivité \(R_0\) en utilisant un modèle épidémique très simple avec saisonnalité.
Considérons le processus de naissance et de mort avec des coefficients \(a(t)\) et \(b(t)\) qui sont \(\theta\)-périodiques: \[\frac{dW_k}{dt} = a(t)\, (k-1)\, W_{k-1}(t) - [a(t)+b(t)]\, k\, W_k(t) + b(t)\, (k+1)\, W_{k+1}(t),\quad k\geq 1\] et \(dW_0/dt = b(t)\, W_1(t)\). Ici \(W_k(t)\) est la probabilité d'avoir k personnes infectées au temps t. Si \(Z\) personnes infectées (\(Z\geq 1\)) sont introduites ou présentes au temps T, alors \(W_Z(T)=1\) et \(W_k(T)=0\) pour \(k\neq Z\). La probabilité \(W_0(t)\) d'extinction au temps t se calcule en résolvant l'équation aux dérivées partielles du premier ordre vérifiée par la fonction génératrice \(g(t,x)=\sum_{k\geq 0} W_k(t) x^k\). Le résultat, donné par (Bartlett, 1960), reste valide même si \(a(t)\) et \(b(t)\) ne sont pas périodiques: \[W_0(t)=\Bigl [1-\frac{ e^{-\int_T^t (b(\tau)-a(\tau))\, d\tau}}{1+ \int_T^t a(\tau)\, e^{-\int_{\tau}^t (b(\sigma)-a(\sigma))\, d\sigma} d\tau}\Bigr ]^Z . \] Noter que l'espérance \(I(t)\) du nombre de personnes infectées au temps \(t\) est donnée par \[I(t)=\sum_{k\geq 1} k\, W_k(t),\quad \frac{dI}{dt}=a(t)\, I(t)-b(t)\, I(t).\] Comme on peut le deviner avec cette équation différentielle, et comme le montre (Bacaër et Guernaoui, 2006, §5) pour des fonctions \(a(t)\) et \(b(t)\) qui sont périodiques, la reproductivité \(R_0\) définie dans la section 2 est donnée par \[R_0=\Bigl (\int_0^\theta a(\tau)\, d\tau \Bigr ) / \Bigl (\int_0^\theta b(\tau)\, d\tau \Bigr )\, .\] Remarquer que si \(R_0 < 1\), alors \(W_0(t)\to 1\) quand \(t\to +\infty\) : l'épidémie s'éteint. Si \(R_0 > 1\), alors \[W_0(t)\mathop{\longrightarrow}_{t\to +\infty} \Bigl [1 - 1/\int_T^\infty a(\tau)\, e^{\int_T^\tau (b(\sigma)-a(\sigma))\, d\sigma}\, d\tau\Bigr ]^Z\] et il existe une certaine probabilité que l'épidémie persiste.
Ainsi la reproductivité \(R_0\) sert aussi de seuil entre d'une part la situation où l'épidémie s'éteint avec une probabilité égale à 1 quel que soit le temps initial d'introduction du premier cas infecté, et d'autre part la situation où l'épidémie s'éteint avec une probabilité strictement comprise entre 0 et 1 et dépendante du temps initial. On peut espérer avoir un phénomène de seuil similaire pour les modèles stochastiques de maladies à vecteurs avec de la saisonnalité. Mais davantage de travail est nécessaire pour vérifier ce point.
Noter que cette section évite l'introduction d'une reproductivité dépendante du temps, « \(R_0(t)\) », définie par exemple pour le cas des maladies à vecteurs par la formule (1) avec \(p\) remplacé par \(p(t)\). Cette expression semble être un bon candidat pour discuter de l'invasion en fonction du temps d'introduction du pathogène. Mais l'exemple de (Hale, 1980, p. 121) mentionné dans (Diekmann et Heesterbeek, 2000, p. 149) suggère déjà que le cas suivant peut bien arriver: \(R_0(t) < 1\) pour tout \(t\) mais l'équilibre sans maladie est instable, c'est-à-dire \(R_0 > 1\) avec \(R_0\) défini comme dans l'article présent. Par ailleurs, \(R_0\) n'est pas en général la moyenne temporelle de « \(R_0(t)\) » (sauf exception comme le cas où \(K(t,x)=a(t)\, e^{-b x}\) étudié dans la section 5.1.1). D'un point de vue biologique, la capacité d'invasion d'un pathogène dans un environnement variant de manière saisonnière dépend évidemment de la date d'introduction du pathogène durant l'année. Comme l'invasion est complètement déterminée par \(R_0\) dans les modèles déterministes, contrairement aux modèles stochastiques, cela donne l'impression que les modèles déterministes sont simplement inadaptés pour discuter de l'invasion en fonction de la date d'introduction du pathogène.
En partant de la définition (9) de \(G(x)\) et en supposant (10), on montre (11) par récurrence. Bien sûr, on ne perd pas en généralité à supposer que \(a_j=1\) pour tout \(j\). Pour \(n=2\), un calcul simple montre que \[G(x) =\int_0^x e^{-\lambda_1\, x_1 -\lambda_2\, (x-x_1)}\, dx_1 =\frac{e^{-\lambda_1\, x}}{\lambda_2-\lambda_1} + \frac{e^{-\lambda_2\, x}}{\lambda_1-\lambda_2}\, .\] Supposons que (11) soit vrai pour un certain entier \(n\). Alors \begin{align*} G(x)&=\int_{\sigma_x^{n+1}} e^{-\lambda_1\, x_1 - \cdots - \lambda_n\, x_n - \lambda_{n+1}\, x_{n+1}}\, d\sigma_x^{n+1}\\ &=\int_0^x \Biggl ( \int_{\sigma_{x-x_{n+1}}^n}\!\!\!\!\!\! e^{-\lambda_1\, x_1 - \cdots - \lambda_n\, x_n}\, d\sigma_{x-x_{n+1}}^{n}\Biggr ) e^{-\lambda_{n+1}\, x_{n+1}}\, dx_{n+1}\\ &=\int_0^x \Biggl ( \sum_{j=1}^n \frac{e^{-\lambda_j\, (x-x_{n+1})}}{\prod_{\substack{k\neq j\\ k\leq n}} (\lambda_k - \lambda_j)} \Biggr ) e^{-\lambda_{n+1}\, x_{n+1}}\, dx_{n+1}\\ &=\sum_{j=1}^n \frac{e^{-\lambda_j\, x}}{\prod_{\substack{k\neq j\\ k\leq n}} (\lambda_k - \lambda_j)} \int_0^x e^{(\lambda_j-\lambda_{n+1}) x_{n+1}} dx_{n+1}\\ &=\sum_{j=1}^n \frac{e^{-\lambda_j\, x}}{\prod_{\begin{subarray}{l} k\neq j\\ k\leq n+1 \end{subarray}} (\lambda_k - \lambda_j)} + e^{-\lambda_{n+1} x} \sum_{j=1}^n \frac{1}{(\lambda_j-\lambda_{n+1}) \prod_{\substack{k\neq j\\ k\leq n}} (\lambda_k - \lambda_j)}\, . \end{align*} Noter que la deuxième somme de la dernière ligne est la décomposition en éléments simples de la fraction rationnelle en \(\lambda_{n+1}\) \[\frac{1}{\prod_{1\leq j \leq n} (\lambda_j-\lambda_{n+1})}\, .\] Donc \[G(x)=\sum_{j=1}^{n+1} \frac{e^{-\lambda_j\, x}}{\prod_{\begin{subarray}{l} k\neq j\\ k\leq n+1 \end{subarray}} (\lambda_k - \lambda_j)},\] et la formule (11) est vraie pour \(n+1\).