\(\mathrm{Institut\ de\ Recherche\ pour\ le\ Développement}\), Bondy, France
nicolas.bacaer@ird.fr
Université Cadi Ayyad, Département de mathématiques, Marrakech, Maroc
On étudie la notion de reproductivité, notée \(R_0\,\), pour les problèmes de dynamique des populations dans des environnements aléatoires. Pour simplifier, on suppose que les environnements successifs suivent une chaîne de Markov. \(\,R_0\,\) est le rayon spectral d'un opérateur de prochaine génération. Sa position par rapport à 1 détermine toujours la croissance ou la décroissance de la population dans les simulations, contrairement à un autre paramètre suggéré dans un article récent [Hernandez-Suarez C, Rabinovich J, Hernandez K (2012) \(\text{Theor. Pop. Biol., doi:10.1016/j.tpb.2012.05.004}\)]. La position de ce dernier paramètre par rapport à 1 détermine la croissance et la décroissance de l'espérance de la population. \(\,R_0\,\) se calcule facilement dans le cas des modèles de population scalaires sans aucune structure. On s'intéresse principalement aux modèles en temps discret mais les modèles en temps continu sont aussi évoqués.
Dans cet article, on considère des modèles de population de la forme \[p(t+1)=X(t)p(t),\quad X(t)=A(t)+B(t),\quad t=0,1,\ldots\] avec \(p(0)\) donné dans \(\mathbb{R}^m\). Le vecteur \(\,p(t)\) représente les différentes composantes de la population. \(A(t)\) et \(B(t)\,\) sont des matrices carrées de taille m à coefficients ≥ 0 pour tout t. \(\,A(t)\) est une matrice de naissance. \(B(t)\,\) est une matrice de survie. Pour simplifier, on suppose que les matrices \(\,(A(t),B(t))\) sont choisies dans une liste finie d'environnements \((A^{(k)},B^{(k)})_{1\leq k\leq K}\). L'environnement de type i est suivi par un environnement de type j \((1\leq i,j\leq K)\) avec une probabilité \(\,M_{i,j}\,\). Avec une probabilité \(\,\mu_i\,\), \((A(0),B(0))\) est de type \(i\). On suppose que la matrice \(\,M=(M_{i,j})\,\) de cette chaîne de Markov est irréductible. Les matrices de survie ont un sens biologique si \[\sum_i B_{i,j}^{(k)}\leq 1,\quad \forall j,\quad \forall k.\] On suppose aussi:
Une vaste littérature existe concernant de tels modèles de population dans un environnement aléatoire (Lewontin et Cohen, 1969 ; Tuljapurkar, 1990). On définit
Bacaër et Guernaoui (2006) ont généralisé la notion classique de reproductivité, aussi appelée taux de reproduction, du cas des environnements périodiques. \(R_0\,\) est un taux asymptotique de croissance par génération (Bacaër et Ait Dads, 2011 et 2012). Thieme (2009, §5.1) et Inaba (2012) ont étudié le cas des environnements déterministes en temps continu mais non périodiques. Dans un article récent, (Hernandez-Suarez et coll., 2012) ont suggéré une adaptation de la reproductivité aux modèles avec des environnements aléatoires. Il semble cependant que la position de leur \(R_0\,\) par rapport à 1 ne décide pas toujours si la population finit par croître ou décroître (un contre-exemple sera présenté ci-dessous). Dans le présent article, on explique comment \(\,R_0\) devrait être calculé pour donner le bon seuil: c'est l'unique solution de l'équation \begin{equation}\tag{3} r(A/R_0,B)=0. \end{equation} Autrement dit, \(R_0\,\) est le nombre par lequel tous les taux de naissance doivent être divisés pour amener la population à la situation critique où ni la croissance exponentielle ni la décroissance exponentielle ne se produit. Une telle caracterisation de \(\,R_0\) a été mise en évidence pour les environnements constants par (Li et Schneider, 2002, théorème 3.1) et pour les environnements périodiques en temps continu ou discret par (Bacaër, 2007, §3.4) et (Bacaër, 2009, section 4).
Dans la section 2, la reproductivité est définie comme le rayon spectral d'un « opérateur de prochaine génération » suivant la terminologie de (Diekmann et Heesterbeek, 2000). D'après la proposition 1, \(R_0 > 1\) si et seulement si \(r > 0\). La proposition 2 montre que la reproductivité peut être calculé en utilisant l'équation (3). La formule pour la reproductivité obtenue pour les environnements périodiques par (Bacaër, 2009) est un cas particulier de l'approche du présent article. La section 3 montre que le paramètre introduit récemment par (Hernandez-Suarez et coll., 2012) détermine la croissance ou le déclin de l'espérance de la population. La section 4 se concentre sur le cas scalaire, pour lequel la reproductivité se calcule facilement. Des exemples numériques sont présentés dans la section 5. La section 6 discute brièvement des modèles en temps continu pour faire le lien avec un récent article (Artalejo et coll., 2012). La conclusion explique la différence entre notre reproductivité et celle de (Hernandez-Suarez et coll., 2012). Il y a la même différence qu'entre l'espérance du taux de croissance et le taux de croissance de l'espérance. Cette différence a été le sujet de nombreuses discussions (Lewontin et Cohen, 1969 ; Tuljapurkar, 1990).
Comme dans le cas périodique (Bacaër et Ait Dads, 2011 et 2012), découpons la population en générations. \(\,q(n,t)\,\) est le vecteur de population appartenant à la génération n au temps t : pour tout \(\,t\geq 0\) et \(n\geq 0\), \begin{align} &q(0,0)=p(0),\quad q(0,t+1)=B(t) q(0,t)\nonumber\\ &q(n+1,0)=0,\quad q(n+1,t+1)=A(t) q(n,t)+B(t)q(n+1,t).\tag{4} \end{align} Noter que le zéro dans le côté droit de l'équation \(q(n+1,0)=0\) est le vecteur nul de \(\mathbb{R}^m\). Si \[p(t)=\sum_{n\geq 0} q(n,t)\] alors \[p(t+1)=(A(t)+B(t))p(t)\quad\forall t\geq 0.\] On définit \[L=\ell^1(\mathbb{N},\mathbb{R}^m)=\left \{ (x(0),x(1),\ldots) ;\quad x(t)\in \mathbb{R}^m\ \forall t\geq 0,\quad \|x\|=\sum_{t\geq 0} \sum_{i=1}^m |x_i(t)| < +\infty\right \}.\] Alors L est un espace de Banach avec cette norme. Noter que (4) s'écrit aussi \begin{equation}\tag{5} q(n+1,0)=0,\quad -B(t)q(n+1,t)+q(n+1,t+1)=A(t)q(n,t). \end{equation} Introduisons les opérateurs \(\mathcal{A}:L\to L\), \(\mathcal{B}:L\to L\) et l'opérateur identité \(\mathcal{I}:L\to L\) avec pour tout \(x\in L\) et \(t\geq 0\), \begin{align*} &(\mathcal{A}x)(0)=0,\quad (\mathcal{A}x)(t+1)=A(t)x(t), \\ &(\mathcal{B}x)(0)=0,\quad (\mathcal{B}x)(t+1)=B(t)x(t),\\ &(\mathcal{I}x)(t)=x(t). \end{align*} Parce que \(A(t)\) et \(B(t)\) sont choisis parmi en ensemble fini de matrices, il est clair que \(\mathcal{A}x\in L\) et \(\mathcal{B}x\in L\) si \(x\in L\). De plus, \(\,\mathcal{A}\) et \(\mathcal{B}\) sont des opérateurs linéaires bornés.
Lemme 1. Le rayon spectral \(\rho(\mathcal{A}+\mathcal{B})\) est égal à \(e^{r(A,B)}\).
Preuve. On définit \(\,\mathcal{X}=\mathcal{A}+\mathcal{B}\). Pour tout \(\,x\in L\) et \(\tau\geq 1\,\), on a \[(\mathcal{X}^\tau x)(t)=0,\quad \quad 0\leq t\leq \tau-1,\] \[(\mathcal{X}^\tau x)(t)=X(t-1)X(t-2)\cdots X(t-\tau) x(t-\tau),\quad \quad t\geq \tau.\] Vus (1) et la formule du rayon spectral, on a \[\rho(\mathcal{X})=\lim_{\tau\to +\infty} \|\mathcal{X}^\tau\|^{1/\tau} = e^{r(A,B)},\] où \(\|\cdot\|\,\) est la norme d'opérateur associée à la norme vectorielle.
Lemme 2. \(r(0,B) < 0\) : la population s'éteint s'il n'y a pas de naissances.
Preuve. On a \(\,\|B^{(k)}\|_1 \leq 1\) pour tout \(k\) et \(\|B^{(\kappa)}\|_1 < 1\). L'environnement \(\,\kappa\) apparaît (si \(t \to +\infty)\) dans une fraction positive \(\pi_\kappa\) des t termes de l'équation (1), parce que la chaîne de Markov est irréductible. Mais \(\,\|\cdot\|_1\,\) est une norme sous-multiplicative. Donc on obtient \(\ r(0,B)\leq \pi_{\kappa} \log \|B^{(\kappa)}\|_1 < 0\).
Parce que \( r(0,B) < 0\), le lemme 1 montre que \(\rho(\mathcal{B}) < 1\). Donc \(\mathcal{I}-\mathcal{B}\) est inversible: si \(y=(\mathcal{I}-\mathcal{B})x\,\), alors \[x=(\mathcal{I}-\mathcal{B})^{-1}y=y+\mathcal{B}y+\mathcal{B}^2y+\cdots\,,\] c'est-à-dire \[x(t)=\sum_{\tau=0}^{t} B(t-1)B(t-2)\cdots B(\tau) y(\tau) \] pour \(t\geq 0\). Si \(\,q_n=(q(n,t))_{t\geq 0}\,\), alors l'équation (5) équivaut à \[(\mathcal{I}-\mathcal{B})q_{n+1}=\mathcal{A} q_n,\] c'est-à-dire \[q_{n+1}=(\mathcal{I}-\mathcal{B})^{-1}\mathcal{A}q_n.\] Parce que \(\,q_0\in L\,\), on a \(q_n\in L\) pour \(n\geq 1\). On définit \(\,g_n=\mathcal{A}q_n\). De cette manière, \(g_n(t+1)=A(t)q(n,t)\) est le vecteur des naissances dues à la génération \(n\) entre les temps \(t\) et \(t+1\). On arrive à la conclusion suivante: \[g_{n+1}=\mathcal{A}q_{n+1}=\mathcal{A}(\mathcal{I}-\mathcal{B})^{-1}g_n.\] Plus explicitement, on a \(g_{n+1}(0)=0\) et l'équation de renouvellement pour les naissances \begin{equation}\tag{6} g_{n+1}(t+1)=\sum_{\tau=0}^t A(t) B(t-1) B(t-2)\cdots B(\tau) g_n(\tau) \end{equation} pour \(t\geq 0\) et \(n\geq 0\).
Définition 1. \(R_0\,\) est le rayon spectral de l'opérateur de prochaine génération \(\mathcal{A}(\mathcal{I}-\mathcal{B})^{-1}\).
Noter l'analogie entre la définition 1 et la présentation de \(\,R_0\,\) pour les modèles en temps continu dans des environnements temporellement hétérogènes de (Thieme, 2009, §5.1) et (Inaba, 2012). On écrit \(\,R_0(A,B)\) pour insister sur la dépendance par rapport aux suites de matrices.
Proposition 1.
Preuve. D'après (Thieme, 2009, théorème 3.10), \(\,R_0(A,B)-1\,\) a le même signe que \(\rho(\mathcal{A}+\mathcal{B})-1\). Mais le lemme 1 dit \(\,\rho(\mathcal{A}+\mathcal{B})=e^{r(A,B)}\). Donc \(R_0(A,B)-1\) a le même signe que \(r(A,B)\).
Proposition 2. Supposons que \(\,R_0(A,B) > 0\). Alors \(R_0(A,B)\) est la solution unique de l'équation \(r(A/R,B)=0\) pour \(R\in (0,+\infty)\).
Preuve. Puisque la reproductivité dépend linéairement de l'ensemble des taux de naissances, on a \[R_0(A/R_0(A,B),B)=1.\] Avec la proposition 1, on a \[r(A/R_0(A,B),B)=0.\] Ainsi l'équation \(\ r(A/R,B)=0\ \) a au moins une solution. Avec (1), \[R \mapsto r(A/R,B),\quad R\in (0,+\infty)\] est une fonction décroissante. En prenant deux fois la dérivée par rapport à R, on voit facilement que \[R\mapsto A_{i,j}(t)/R+B_{i,j}(t) \quad \forall (i,j)\] est une fonction soit identiquement nulle soit log-convexe. Ce point a déjà été utilisé par (Bacaër et Ait Dads, 2012, appendice C). D'aprè (Cohen, 1980, théorème 1), \(\,R\mapsto r(A/R,B)\,\) est une fonction convexe. Donc l'équation \(\,r(A/R,B)=0\,\) ne peut avoir plus qu'une solution. En effet, s'il y avait deux solutions distinctes \(\,R_1\) et \(R_2\) avec \(R_1 < R_2\), la fonction décroissante et convexe \(R\mapsto r(A/R,B)\) serait constante égale à 0 non seulement entre ces deux valeurs mais pour \(R\geq R_1\). Cette fonction de \(\,]0,+\infty[\,\) dans \(\mathbb{R}\,\) est convexe. Elle est aussi continue. Donc \(\,r(A/R,B)\to r(0,B) < 0\) si \(R\to +\infty\). On a ainsi atteint une contradiction.
Remarque 1. La proposition 2 montre qu'en général le calcul de \(R_0\,\) est aussi difficile que le calcul de r, et nécessite plus de temps de calcul car une méthode de dichotomie doit être utilisée.
Remarque 2. Pour les environnements périodiques dans l'ordre \((1,2,\ldots,K)\), (Bacaër, 2009) a montré que \(R_0\) était le rayon spectral de \begin{equation}\tag{7} \left ( \begin{array}{cccc} A^{(1)} & 0 & \cdots& 0\\ 0 & A^{(2)} & & \vdots\\ \vdots & \ddots&\ddots & 0\\ 0 &\cdots & 0 & A^{(K)} \end{array} \right ) \left ( \begin{array}{ccccc} -B^{(1)} & I & 0 & \cdots&0 \\ 0 & -B^{(2)} & I & &0\\ 0&\ddots &\ddots & & \vdots\\ \vdots & \ddots&\ddots & 0& I\\ I &\cdots & 0& 0 & -B^{(K)} \end{array} \right )^{-1}. \end{equation} Bacaër et Ait Dads (2012, Proposition 3) ont insisté sur le fait que ce \(R_0\) est l'unique solution de l'équation \[\rho\left ( \left (\frac{A^{(K)}}{R}+B^{(K)}\right )\cdots \left (\frac{A^{(1)}}{R}+B^{(1)}\right ) \right )=1.\] Avec l'équation (1), le côté gauche ci-dessus est visiblement égal à \(e^{r(A/R,B)}\). On peut donc conclure de la proposition 2 que \(\,R_0\,\) dans (Bacaër, 2009) est identique au \(R_0\) de la définition 1 dans le cas particulier des environnements périodiques (\(M_{i,j}=1\) si \(j=i+1\) et \(1\leq i\leq K-1\), \(M_{K,1}=1\,\), et \(M_{i,j}=0\,\) sinon). On peut présenter \(\,R_0\) dans un environnement périodique comme le rayon spectral de \begin{equation}\tag{8} \left ( \begin{array}{ccccc} 0 & 0 & \cdots&0 & A^{(K)}\\ A^{(1)} & 0 & & &0\\ 0&\ddots &\ddots & & \vdots\\ \vdots & \ddots&\ddots & 0& 0\\ 0 &\cdots & 0& A^{(K-1)} & 0 \end{array} \right ) \left ( \begin{array}{ccccc} I & 0 & \cdots&0 & -B^{(K)}\\ -B^{(1)} & I & & &0\\ 0&\ddots &\ddots & & \vdots\\ \vdots & \ddots&\ddots & I& 0\\ 0 &\cdots & 0& -B^{(K-1)} & I \end{array} \right )^{-1} \end{equation} dont on voit facilement qu'il est égal au rayon spectral de (7) (Hernandez-Suarez et coll., 2012, section 5). D'après (Bacaër et Ait Dads, 2012), ce rayon spectral est é au rayon spectral de \(\,A(I-B)^{-1}\) (Cushing et Zhou, 1994 ; Caswell, 2001) lorsque l'environnement est constant, avec \(A^{(k)}=A\) et \(B^{(k)}=B\,\) pour tout k.
Proposition 3. La définition de \(\,R_0\) ci-dessus est indépendante de la suite aléatoire particulière \((A(t),B(t))_{t\geq 0}\,\), qui suit la chaîne de Markov. Donc \(\, R_0\) peut être appelé la reproductivité du modèle.
Preuve. Soient \(\,(A(t),B(t))\) et \((A'(t),B'(t))\, \) deux suites d'environnements qui suivent la chaîne de Markov. Les repoductivités correspondantes sont \(\,R_0(A,B)\) et \(R_0(A',B')\). On souhaite montrer que \(R_0(A,B)=R_0(A',B')\). Avec la proposition 2, on a \(r(A/R_0(A,B),B)=0\) et \(r(A'/R_0(A',B'),B')=0\). Mais les taux de croissance sont indépendants de la suite particulière d'environnements (Tuljapurkar, 1990). Donc \[0=r(A/R_0(A,B),B)=r(A'/R_0(A,B),B').\] \(R_0(A,B)\) et \(R_0(A',B')\) sont solutions de \(r(A'/R,B')=0\). D'après la proposition 2, \(R_0(A,B)=R_0(A',B')\).
Un article récent, (Hernandez-Suarez et coll., 2012) suggère de définir la reproductivité comme le rayon spectral de la matrice \begin{equation}\tag{9} \left (\begin{array}{ccc} M_{1,1} A^{(1)} &\cdots & M_{K,1} A^{(K)}\\ \vdots & & \vdots\\ M_{1,K} A^{(1)} & \cdots &M_{K,K} A^{(K)}\end{array} \right ) \left [ I - \left (\begin{array}{ccc} M_{1,1} B^{(1)} &\cdots & M_{K,1} B^{(K)}\\ \vdots & & \vdots\\ M_{1,K} B^{(1)} & \cdots &M_{K,K} B^{(K)}\end{array} \right ) \right ]^{-1}, \end{equation} où \(I\,\) est la matrice identité de taille convenable. On note ce rayon spectral \(\,R_*\) pour éviter toute confusion.
Dans la littérature sur les environnements markoviens, il est connu que \begin{equation}\tag{10} \log \mu = \lim_{t\to +\infty} \frac{\log \mathbb{E} [|p(t)|]}{t} \end{equation} existe (\(|\cdot|\,\) désigne la somme des composantes). De plus, μ est le rayon spectral de \(\,D(M'\otimes I)\), où
Proposition.
Preuve. On a \[D(M'\otimes I) = \left (\begin{array}{ccc} M_{1,1} (A^{(1)}+B^{(1)}) &\cdots & M_{K,1} (A^{(K)}+B^{(K)})\\ \vdots & & \vdots\\ M_{1,K} (A^{(1)}+B^{(1)}) & \cdots &M_{K,K} (A^{(K)}+B^{(K)})\end{array} \right ). \] Cette matrice est égale à \(A^*+B^*\), où \[A^*= \left (\begin{array}{ccc} M_{1,1} A^{(1)} &\cdots & M_{K,1} A^{(K)}\\ \vdots & & \vdots\\ M_{1,K} A^{(1)} & \cdots &M_{K,K} A^{(K)}\end{array} \right ), \] et \(B^*\,\) est définie de la même manière en remplaçant A par B. D'après (Thieme, 2009, théorème 3.10), \(\rho(A^*+B^*)-1\) et \(\rho(A^*(I-B^*)^{-1})-1\,\) ont le même signe. Mais \(\,\mu=\rho(A^*+B^*)\) et \(R_*=\rho(A^*(I-B^*)^{-1})\).
Remarque 3. Dans un environnement périodique, on a \(\,R_0=R_*\), comme on peut le voir en comparant les matrices (8) et (9).
Si \(A(t)\) et \(B(t)\) sont scalaires et si les environnements sont indépendants et identiquement distribués, alors l'équation (2) et la proposition 2 montrent que \[\sum_{k=1}^K m_k \log \left (\frac{A^{(k)}}{R_0}+B^{(k)}\right )=0,\] ou de manière équivalente \[\prod_{k=1}^K \left (\frac{A^{(k)}}{R_0}+B^{(k)}\right )^{m_k}=1.\]
Considérons maintenant le cas plus général d'une dépendance markovienne entre les environnements successifs. Rappelons que \(M=(M_{i,j})\,\) est une matrice de probabilités de transition. La chaîne étant irréductible, soit π la distribution stationnaire du temps passé dans les différents environnements: \[\pi_j = \sum_i \pi_i M_{i,j}\quad \forall j, \quad \sum_j \pi_j=1.\] (Haccou et coll., 2005, §2.9.2) indiquent que le taux de croissance est \[r(A,B)=\sum_k \pi_k \log(A^{(k)}+B^{(k)})\] Pour preuve, noter simplement que \[\log p(t)=\sum_{\tau=0}^{t-1} \log X(\tau) + \log p(0).\] Si \(t\to +\infty\,\), le nombre de termes égaux à \(\log(A^{(k)}+B^{(k)})\) dans la somme sur τ est \(\pi_k\, t+o(t)\). Ainsi donc, la proposition 2 montre que \(\,R_0\) est la solution de \begin{equation}\tag{11} \prod_{k=1}^K \left (\frac{A^{(k)}}{R_0}+B^{(k)}\right )^{\pi_k}=1. \end{equation} Par conséquent, \(R_0\) se calcule facilement, par exemple avec une méthode de dichotomie.
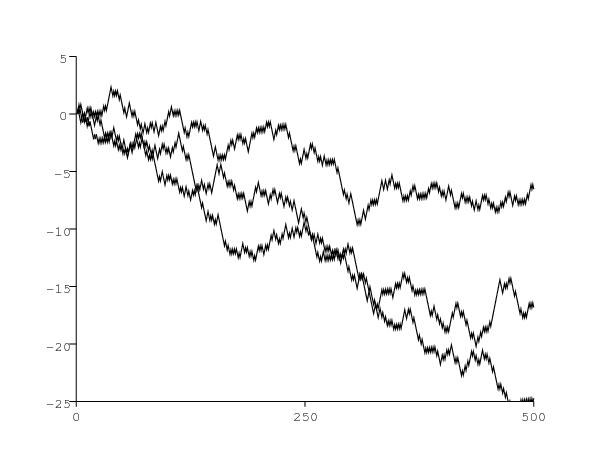
Comme premier exemple, considérons une population scalaire (\(m=1\)) et supposons qu'il y ait deux environnements (\(K=2\)): \[A^{(1)}=1,\ B^{(1)}=\mbox{0,5}\, ,\ A^{(2)}=\mbox{0,1}\, ,\ B^{(2)}=\mbox{0,58}\, ,\ M=\left (\begin{array}{ccc} \mbox{0,3} & &\mbox{0,7}\\ \mbox{0,6} & &\mbox{0,4} \end{array}\right ).\] La distribution stationnaire est \((\pi_1,\pi_2)=(6/13,7/13)\). L'équation (11) donne \(\,R_0\simeq \mbox{0,949} < 1\) : la population s'éteint presque sûrement. Pour un tel exemple, l'équation (9) donne \(\,R_*\simeq \mbox{1,050} > 1\). Plusieurs simulations de ce modèle partant de \(\ p(0)=1\ \) illustrent cela. La figure 1 suggère que le processus est effectivement sous-critique. Les valeurs des paramètres sont choisies précisément pour que \(R_0 < 1\) et \(R_* > 1\). Cependant il semblerait que dans de nombreux autres cas, les deux paramètres soient du même côté de 1 et ne diffèrent que très peu, la différence étant souvent inférieure à 1%. Bien qu'une telle différence puisse sembler biologiquement insignifiante, elle garde de l'importance pour démontrer mathématiquement des résultats de seuil.

Comme second exemple, considérons un modèle avec deux types et deux environnements: \[A^{(1)}=\left (\begin{array}{ccc} \mbox{0,1} &&2\\ 0 &&0 \end{array}\right ),\quad B^{(1)}=\left (\begin{array}{ccc} 0& &0\\ \mbox{0,1} &&0 \end{array}\right ),\] \[A^{(2)}=\left (\begin{array}{ccc} 1 &&\mbox{0,3}\\ 0 &&0 \end{array}\right ),\quad B^{(2)}=\left (\begin{array}{ccc} 0&& 0\\ \mbox{0,7}&& 0 \end{array} \right ),\quad M=\left (\begin{array}{ccc} \mbox{0,5} &&\mbox{0,5}\\ \mbox{0,5} &&\mbox{0,5} \end{array}\right ).\] Noter que les matrices \(A^{(k)}+B^{(k)}\) pour \(k=1,2\,\) sont des matrices de Leslie et que les environnements sont indépendants et identiquement distribués. La formule (9) donne \(\,R_*=\mbox{1,01} > 1\). Si \(p(0)=(1\, 1)'\), si l'on estime le taux de croissance r avec la formule \[\frac{1}{t} \log (|p(t)|/|p(0)|)\] avec t=5000, et si l'on itère le processus 1000 fois, on trouve que la moyenne du taux de croissance est \(-\mbox{0,1021}\) avec une erreur standard de \(\mbox{0,0074}\). Ceci suggère r < 0 et donc \(\,R_0 < 1\). Pour estimer la reproductivité numériquement, on utilise la proposition 2 : on divise \(\,A^{(k)}\) pour \(k=1,2\,\) par R et on estime le nouveau taux de croissance. Avec \(\,R=\mbox{0,84}\,\), on trouve \(r\simeq \mbox{0,0135}\) avec une erreur standard de \(\mbox{0,0072}\), ce qui suggère que \(r > 0\). Avec \(R=\mbox{0,88}\,\), on trouve \(r\simeq -\mbox{0,0168}\) avec une erreur standard de \(\mbox{0,0071}\), ce qui suggère que \(r < 0\). Il semblerait donc que \(\mbox{0,84} < R_0 < \mbox{0,88}\).
Pour le même exemple, on peut aussi utiliser directement la définition de la reproductivité comme rayon spectral de l'opérateur \[\Omega=\mathcal{A}(\mathcal{I}-\mathcal{B})^{-1}.\] Attention cependant que cet opérateur n'a pas de valeur propre non nulle, comme dans le cas en temps continu étudié par (Inaba, 2012, lemme 9). Mais on peut calculer \(\,g_n\,\) pour n grand et estimer la reproductivité avec \(\,\sqrt[n]{\|g_n\|/\|g_0\|}\). Dans notre exemple, noter que \(\,B^{(k)}B^{(k')}=0\) pour tout \(k,k'=1,2\) et \(g_0(t)=0\) pour tout \(t\geq 3\). L'équation de renouvellement (6) montre que si \(\,g_{n}(t)=0\) pour tout \(t\geq \tau\,\), alors \(g_{n+1}(t)=0\) pour tout \(t\geq \tau+2\). Donc \(g_n(t)=0\) pour tout \(t\geq 2n+3\). Pour calculer \(\,g_n\,\), il suffit donc de considérer l'opérateur \(\Omega\) sur le sous-espace de dimension finie \(\ell^1(\{0,1,\ldots,2n+2\},\mathbb{R}^2)\). Avec n=1000, on a choisi 10 suites aléatoires d'environnements. On a trouvé des estimations de la reproductivité avec une moyenne de 0,86 et une erreur standard de 0,015, en accord avec l'estimation déjà obtenue.
Esquissons une théorie similaire pour les modèles linéaires de population en temps continu dans un environnement aléatoire ergodique. Prenons par exemple un modèle \begin{equation}\tag{12} \frac{dp}{dt} = (A(t)-B(t))p(t), \end{equation} où
La reproductivité peut être définie comme le rayon spectral de l'opérateur de renouvellement \(\mathcal{K}\) sur \(L^1((0,\infty),\mathbb{R}^m)\) donné par \[(\mathcal{K}u)(t)= \int_0^t K(t,x) u(t-x)\, dx,\] où le noyau est donné par \(K(t,x)=A(t) C(t,x)\) et \(C(t,x)\,\) est la matrice de survie entre les temps \(t-x\,\) et t : \[C(t,x)=Z(t), \quad \frac{dZ}{ds} = -B(s)Z(s) \quad (t-x < s < t), \quad Z(t-x)=I\] (la matrice identité). En effet, on sait d'après (Bacaër et Ait Dads, 2011, lemme 2) que le vecteur de naissances par unité de temps dues à la génération n vérifie une relation de récurrence impliquant cet opérateur linéaire, qui est semblable à l'équation (6). Pour une discussion du lien entre le rayon spectral de cet opérateur et la reproductivité mais pour les modèles déterministes, voir (Inaba, 2012, section 4). Si \(\,R_0 > 0\) alors la reproductivité peut encore une fois être caractérisé par le fait que \(\lambda_1(A/R_0,B)=0\,\), comme dans la proposition 2. Le rayon spectral \(R_0\) de \(\mathcal{K}\) est presque sûrement indépendant de la suite aléatoire particulière d'environnements, comme dans la proposition 3.
Si \(p(t)\) est une population scalaire, alors on a \[\lambda_1(A,B)=\langle A \rangle - \langle B \rangle,\] où par exemple \[\langle A \rangle = \lim_{t\to \infty} \frac{1}{t} \int_0^t A(s)\, ds.\] Donc \[R_0 = \frac{\langle A \rangle}{\langle B \rangle}\] comme dans le travail de (Cordova-Lepe et coll., 2012) pour un modèle à coefficients presque périodiques. Pour le vecteur ligne \(\,v=(1\ 1 \ldots 1)\,\), on a \(\,dv/dt=0=v Q(t)\,\). On peut montrer, suivant (Perthame, 2007, §6.3.2), qu'il existe une unique solution T-périodique positive \(\,u(t)\) de \[\frac{du}{dt} = Q(t) u(t),\quad \sum_i u_i(t)=1.\] La loi des grands nombres pour les chaînes de Markov montre que \[\langle A \rangle = \frac{1}{T}\int_0^T \sum_k u_k(s) A^{(k)}\, ds.\] Donc \[R_0=\frac{\int_0^T \sum_k u_k(s) A^{(k)}\, ds}{\int_0^T \sum_k u_k(s) B^{(k)}\, ds}\, .\] Si \(Q(t)\,\) ne dépend pas de t, alors il existe un unique vecteur u tel que \[Qu=0,\quad \sum_i u_i=1.\] Donc \[R_0=\frac{\sum_k u_k A^{(k)}}{\sum_k u_k B^{(k)}}.\] Cette formule pour \(R_0\) est la même que celle de (Artalejo et coll., 2012, §4.1) pour « \(R_0^{ARA}\) ».
La différence entre le \(R_0\) du présent article et le « \(R_0\,\) » (noté ici \(R_*\)) dans (Hernandez-Suarez et coll., 2012) est semblable à la différence entre d'une part le taux de croissance « stochastique » (1), qui est aussi égal à l'espérance du taux de croissance de la population \[r=\lim_{t\to +\infty} \mathbb{E}\left [\frac{\log |p(t)|}{t}\right ],\] d'autre part le taux de croissance de l'espérance de la population (10) (Lewontin et Cohen, 1969 ; Tuljapurkar, 1990). C'est la position de r par rapport à 0, ou celle de \(\,R_0\,\) par rapport à 1, qui décide si la population est sous-critique ou surcritique dans les simulations. Cependant \(\,\log \mu\) et \(R_*\) sont beaucoup plus faciles à calculer dans les environnements markoviens pour les populations structurées (non scalaires): ils sont donnés par les rayons spectraux de simples matrices.
On remercie Sylvie Méléard, Odo Diekmann et particulièrement Carlos Hernandez-Suarez pour avoir stimulé notre intérêt pour les environnements aléatoires.