
Institut de Recherche pour le Développement, Bondy, France
nicolas.bacaer@ird.fr
Université Cadi Ayyad, Département de mathématiques, Marrakech, Maroc
Pour des processus de branchement avec plusieurs types dans un environnement périodique, on montre que la probabilité d'extinction est égale à 1 si et seulement si la reproductivité est inférieure ou égale à 1. La démonstration utilise des résultats sur le comportement asymptotique des systèmes coopératifs d'équations différentielles. En épidémiologie, la probabilité d'extinction peut être utilisée comme une mesure périodique du risque épidémique. Comme exemple, on étudie un modèle épidémique SEIR linéarisé et des données sur une épidémie de rougeole en France. On discute aussi de modèles en temps discret avec des applications potentielles en biologie de la conservation.
Kendall (1948) a étudié les processus de naissance et de mort à un seul type dans un environnement variable. On définit
Les processus de naissance et de mort à plusieurs types dans un environnement constant sont bien connus (Athreya et Ney, 1972, chapitre V). Pour les environnements périodiques, Klein et Macdonald (1980) ont étudié l'espérance et la variance des populations de différents types mais pas la probabilité d'extinction. Voir aussi (Parham et Michael, 2011). Le système d'équations pour les espérances est de la forme \[\frac{dI}{dt} = (A(t) - B(t))\,I(t),\]
Jagers et Nerman (1985) ont étudié les processus de branchement en temps continu dans un environnement périodique avec une mortalité et une fécondité dépendantes de l'âge, mais seulement pour un seul type. Le seuil était formulé en terme de paramètre malthusien.
En suivant le livre d'Anderson et May (1991), de nombreux modélisateurs utilisent la reproductivité pour décrire le seuil des modèles de population et en particulier des modèles épidémiques. Bacaër et Guernaoui (2006, section 5) ont adapté la définition de la reproductivité comme rayon spectral d'un opérateur de prochaine génération de Diekmann et Heesterbeek (2000) au cas des modèles périodiques. Ils ont aussi montré que \[{R}_0= \frac{\int_0^T a(t)\, dt}{\int_0^T b(t)\, dt}\] pour les modèles à un type comme ci-dessus. Ainsi Bacaër (2007, §5.2) a reformulé la propriété de seuil pour les processus linéaires de naissance et de mort à un seul type dans un environnement périodique comme suit: \(\omega=1\) si \({R}_0\leq 1\), tandis que \(\omega < 1\) si \({R}_0 > 1\).
Pour les populations à plusieurs types étudiées par Klein et Macdonald (1980), \({R}_0\) peut être défini comme le rayon spectral de l'opérateur intégral \[u(t) \mapsto A(t) \int_0^\infty C(t,t-x)\, u(t-x)\, dx\] sur l'espace des fonctions continues périodiques, de période T. Ici \[C(t,t-x)=Z(t)Z(t-x)^{-1}, \quad \frac{dZ}{dt}=-B(t) Z(t),\quad Z(0)=\mathbb{I}\] (la matrice identité). Allen et Lahodny (2012) ont récemment résumé les liens entre la reproductivité et la probabilité d'extinction pour les processus de naissance et de mort à plusieurs types mais dans un environnement constant.
Dans cet article, on considère la même classe de processus de branchement à plusieurs types dans un environnement périodique que Klein et Macdonald (1980). On montre que la probabilité d'extinction \(\omega\) est égale à 1 si et seulement si \(R_0\leq 1\). Ceci étend les résultats concernant les populations à un seul type dans un environnement périodique et ceux concernant les populations à plusieurs types dans un environnement constant. Dans la preuve de la section 2, on voit que le système d'équations différentielles non linéaires donnant la probabilité d'extinction est étroitement relié à au système linéaire ci-dessus pour le vecteur des espérances. La démonstration utilise ensuite des résultats concernant le comportement asymptotique des systèmes coopératifs d'équations différentielles. Comme exemple on considère dans la section 3.1 un modèle épidémique SEIR et sa linéarisation. On calcule la probabilité d'extinction en utilisant des données d'une épidémie de rougeole en France. La section 3.2 discute du cas des modèles en temps discret, qui sont utilisés en biologie de la conservation pour estimer la probabilité d'extinction d'espèces réintroduites. La section 4 suggère d'utiliser la probabilité de non-extinction 1−ω comme mesure périodique du risque épidemique en plus des autres techniques qui ont été proposées ces dernières années.
Considérons d'abord un modèle linéaire déterministe de population \begin{equation}\tag{2} \frac{dI}{dt} = (A(t) - B(t))I(t), \end{equation}
Considérons maintenant le processus de naissance et de mort à plusieurs types associé à (2). \(p(t,i_1,\ldots,i_m)\) est la probabilité d'avoir \(i_k\) personnes dans le compartiment \(I_k\) au temps t pour \(1\leq k\leq m\ :\) \begin{align*} \frac{d}{dt}p(t,i_1,\ldots,i_m)=&\sum_k \Bigl [A_{kk}(i_k-1) + \sum_{\ell\neq k} A_{k\ell} i_\ell \Bigr ] p(t,i_1,\ldots,i_k-1,\ldots,i_m)\\ &+\sum_{k\neq \ell} b_{k\ell}\, (i_\ell+1)\, p(t,i_1,\ldots,i_k-1,\ldots,i_\ell+1,\ldots,i_m)\\ &+\sum_k b_{k,k}\, (i_k+1)\, p(t,i_1,\ldots,i_k+1,\ldots,i_m)\\ &- \sum_{k,\ell} (A_{k\ell}+b_{k\ell})\, i_\ell\, p(t,i_1,\ldots,i_m), \end{align*} où la dépendance en temps des coefficients a été omise. Ce système suit ce qui se passe pendant un petit intervalle de temps dt. Si par exemple le système est dans l'état \((i_1,\ldots,i_{k}-1,\ldots,i_m)\), alors la probabilité qu'une personne de type k engendre une nouvelle personne du même type est \(A_{kk}(i_k-1) dt\). Dans ce cas, le système se retrouve dans l'état \((i_1,\ldots,i_{k},\ldots,i_m)\). Prenons comme condition initiale \[p(t_0,i_1,\ldots,i_m)=\left \{\begin{array}{ll} 1, &\quad (i_1,\ldots,i_m)=(I_1(t_0),\ldots,I_m(t_0)),\\ 0, &\quad (i_1,\ldots,i_m) \neq (I_1(t_0),\ldots,I_m(t_0)). \end{array} \right.\] L'objectif est de calculer la probabilité d'extinction \[\omega = \lim_{t\to +\infty} p(t,0,\ldots,0).\] Rappelons que l'équation (2) est vérifiée par l'espérance du nombre de personnes dans les différents compartiments (Klein et Macdonald, 1980).
Proposition.
Preuve. La fonction génératrice \[g(t,x_1,\ldots,x_m)=\sum_{i_1,\ldots,i_m\geq 0} p(t,i_1,\ldots,i_m) x_1^{i_1}\ldots x_m^{i_m}\] est solution de l'équation \[\frac{\partial g}{\partial t}=\sum_{k,\ell} \bigl [A_{k\ell}(t) x_\ell - B_{k\ell}(t)](x_k-1) \, \frac{\partial g}{\partial x_\ell} \, ,\] avec la condition initiale \begin{equation}\tag{3} g(t_0,x_1,\ldots,x_m)=x_1^{I_1(t_0)}\cdots x_m^{I_m(t_0)}. \end{equation} Le courbes caractéristiques de cette équation aux dérivées partielles linéaire du premier ordre sont \begin{equation}\tag{4} \frac{dX_\ell}{dt} = \sum_k \bigl [A_{k\ell}(t)X_\ell-B_{k\ell}(t)\bigr ] (1-X_k) \, . \end{equation} Alors \[\frac{d}{dt}[g(t,X_1(t),\ldots,X_m(t))]=0\] et \begin{equation}\tag{5} g(t,X_1(t),\ldots,X_m(t))=g(t_0,X_1(t_0),\ldots,X_m(t_0)). \end{equation} On définit \(X^{(\tau)}(t)\), solution du système (4) avec \[X^{(\tau)}(\tau)=0.\] En utilisant (3) et \(t=\tau\) dans (5), on obtient \begin{equation}\tag{6} p(\tau,0,\ldots,0)=g(\tau,0,\ldots,0)=(X_1^{(\tau)}(t_0))^{I_1(t_0)} \cdots (X_m^{(\tau)}(t_0))^{I_m(t_0)}. \end{equation} Donc la probabilité d'extinction est donnée par \[\omega= (\omega_1)^{I_1(t_0)} \cdots (\omega_m)^{I_m(t_0)},\quad \omega_\ell = \lim_{\tau \to +\infty} X_\ell^{(\tau)}(t_0).\] Le problème se ramène par conséquent à l'étude du système d'équations différentielles (4). On définit \begin{equation}\tag{7} Y_\ell^{(\tau)}(s)=1-X_\ell^{(\tau)}(\tau-s). \end{equation} On obtient \begin{equation}\tag{8} \frac{dY_\ell^{(\tau)}}{ds}(s) = \sum_k \left [A^*_{\ell k}(\tau-s)\, \left (1-Y^{(\tau)}_\ell(s)\right ) - B^*_{\ell k}(\tau-s) \right ] Y^{(\tau)}_k(s) \, . \end{equation} \(A^*\) et \(B^*\) sont les matrices transposées de \(A\) et \(B\). La condition initiale est \[Y_\ell^{(\tau)}(0)=1,\quad \forall\, \ell.\] L'hypothèse (H3) implique que \begin{equation}\tag{9} Y_\ell^{(\tau)}(s)=Y_\ell^{(\tau+T)}(s),\quad \forall\, s,\quad \forall\, \tau,\quad \forall\, \ell. \end{equation}
Pour appliquer le théorème 2.3.4 de (Zhao, 2003), vérifions les analogues des hypothèses (A1)-(A4) du théorème 3.1.2 de cette référence, à ceci près que le système (8) évolue dans le cube unité \(K=[0,1]^m\) au lieu de \(\mathbb{R}_+^m\). Tout d'abord, le système (8) laisse K invariant. En effet, si \(F_\ell(s,Y^{(\tau)}(s))\) est le côté droit de (8), et si \(Y\in K\), \begin{align} &Y_\ell=0\ \Rightarrow F_\ell(s,Y) = \sum_{k\neq \ell} \Bigl (A^*_{\ell k}(\tau-s) + b_{k \ell}(\tau-s) \Bigr ) Y_k \geq 0\, ,\nonumber\\ &Y_\ell=1\ \Rightarrow F_\ell(s,Y) = - b_{\ell\ell}(\tau-s) - \sum_{k\neq \ell} b_{k\ell}(\tau-s) (1-Y_k) < 0\, ,\tag{10} \end{align} l'inégalité stricte dans (10) étant due à (H4). La proposition B.7 de (Smith et Waltman, 1995) montre que pour toute condition initiale dans K au temps \(s_0\), la solution correspondante de (8) reste ensuite dans K. Par ailleurs, d'après (10), \[(\exists \ell,\quad Y_\ell(s_0)=1)\quad \Rightarrow \quad (\forall\, s > s_0,\quad Y_\ell(s) < 1).\]
Le système (8) est coopératif dans K : \[Y\in K \quad \Rightarrow \quad \forall k\neq \ell,\quad \frac{\partial F_\ell}{\partial Y_k}(s,Y) = A^*_{\ell k}(\tau-s)\, (1-Y_\ell) + b_{k\ell}(\tau-s)\geq 0\, .\] D'après le théorème de Kamke (Smith et Waltman, 1995, théorème B.1), les applications de Poincaré du système (8) sur K sont monotones. L'hypothèse (H2) implique que la matrice jacobienne \[\bigl (\frac{\partial F_\ell}{\partial Y_k}(s,Y)\bigr )\quad \forall s, \quad \forall Y \in \widehat{K}=\{Y\in K: \ Y_\ell < 1 \ \forall\,\ell\} \] est irréductible. Cette propriété et l'inégalité stricte (10) impliquent que les applications de Poincaré de (8) dans K, qui projettent la solution du temps \(s_0\) jusqu'au temps \(s_0+T\), sont en réalité fortement monotones. En effet, si \[Y(s_0)\neq Y'(s_0),\quad Y(s_0)\leq Y'(s_0),\] c'est-à-dire \(Y_\ell(s_0)\leq Y'_\ell(s_0)\) pour tout \(\ell\), alors on a \[Y(s_0+T/2)\leq Y'(s_0+T/2),\] les deux vecteurs étant différents et dans \(\widehat{K}\). En utilisant l'irréductibilité dans \(\widehat{K}\), le théoreme B.3 de (Smith et Waltman, 1995) montre que \[Y_\ell(s_0+T) < Y'_\ell(s_0+T)\quad \forall \, \ell.\]
Le système (8) est strictement sous-homogène. En effet, pour tout \(\alpha \in (0,1)\) et \(Y\in K\) avec \(Y_\ell > 0\) pour tout \(\ell\), on a \[F_\ell(s,\alpha Y)=\alpha\, F_\ell(s,Y) + \alpha(1-\alpha) \sum_k A^*_{\ell k}(\tau-s) Y_\ell Y_k\, .\] Par conséquent, \(F_\ell(s,\alpha Y)\geq \alpha\, F_\ell(s,Y)\) et \(F(s,\alpha Y)\neq \alpha\, F(s,Y)\) d'après l'hypothèse (H1).
On a \(F(s,0)=0\). On définit \(f(s,Y)\), la partie linéaire de \(F(s,Y)\) près de \(Y=0\) \[f_\ell(s,Y)= (M^*(\tau-s)Y)_\ell,\quad \quad F_\ell(s,Y) = f_\ell(s,Y) - \sum_k A^*_{\ell k}(\tau-s) Y_\ell Y_k\, .\] Par conséquent \(F_\ell(s,Y)\leq f_\ell(s,Y)\) et, vu l'hypothèse (H1), \(F(s,Y)\neq f(s,Y)\) si \(Y_\ell > 0\) pour tout \(\ell\).
Le multiplicateur de Floquet dominant du système \(\frac{dY}{ds}=M^*(\tau-s)Y\) est le même que celui du système \(\frac{dY}{dt}=M(t)Y\). En effet, observons les solutions (avec la matrice identité comme condition initiale au temps 0) \(\Phi_1(t)\), \(\Phi_2(t)\), \(\Phi_3(t)\) et \(\Phi_4(t)\) de \[\frac{dY}{dt}=M(t)Y,\quad \frac{dY}{dt}=M(\tau+t)Y,\quad \frac{dY}{dt}=-M^*(\tau+t)Y,\quad \frac{dY}{ds}=M^*(\tau-s)Y.\] Le deuxième système est le même que le premier mais décalé dans le temps. Le troisième est le transposé du deuxième. Le quatrième est identique au troisième sauf que le temps est renversé. Donc \[ \Phi_2(T)=\Phi_1(\tau) \Phi_1(T) (\Phi_1(\tau))^{-1} ,\quad \ \Phi_3(T)=((\Phi_2(T))^*)^{-1},\quad \ \Phi_4(T)=(\Phi_3(T))^{-1} \] (Hsieh et Sibuya, 1999). Par conséquent, le rayon spectral \(\rho_0\) de \(\Phi_1(T)\) est égal à celui de \(\Phi_4(T)\), comme annoncé.
Appliquons le théorème 2.3.4 de (Zhao, 2003). Avec \(\rho_0\leq 1\), l'équilibre 0 du système (8) est globalement asymptotiquement stable dans K. En particular, \[Y^{(\tau)}(s)\mathop{\longrightarrow}_{s\to +\infty} 0.\] Avec \(\rho_0 > 1\), le système (8) a une unique solution strictement positive, périodique de période T, qui est globalement asymptotiquement stable dans \(K\setminus \{0\}\) et attire \(Y^{(\tau)}(s)\) si \(s\to +\infty\).
Avec (6) on voit que \[X_\ell^{(\tau)}(t_0)=p(\tau,0,\ldots,0)\] si \[I_\ell(t_0)=1,\quad I_k(t_0)=0\quad \forall\, k\neq \ell.\] La fonction \(\tau\mapsto p(\tau,0,\ldots,0)\) est visiblement croissante, par exemple parce que \[\frac{d}{dt}p(t,0,\ldots,0) = \sum_k b_{kk}\, p(t,0,\ldots,1,\ldots,0)\geq 0.\] Cette fonction est aussi ≤ 1, étant une probabilité. Donc \(X_\ell^{(\tau)}(t_0)\) converge vers une limite \(\omega_\ell\leq 1\) si \(\tau\to +\infty\).
Revenons au système (4) où le temps est renversé. On a \(X_\ell^{(\tau)}(t_0)=1-Y_\ell^{(\tau)}(\tau-t_0)\). En utilisant (9), on a pour tout \(\tau > t_0\) et tout entier n \[X_\ell^{(\tau+nT)}(t_0)=1-Y_\ell^{(\tau)}(\tau+nT-t_0).\] Avec \(n\to +\infty\), on conclut que \(\omega_\ell=1\) si \(\rho_0 \leq 1\), tandis que \(\omega_\ell < 1\) si \(\rho_0 > 1\).
Pour conclure la démonstration, il reste à rappeler le lien entre le taux de croissance \(r_0\) (tel que \(\rho_0=e^{r_0T}\)) et la reproductivité \({R}_0\) (Bacaër et Guernaoui, 2006 ; Bacaër et Ait Dads, 2011 ; Thieme, 2009) : \(r_0\leq 0\) si et seulement si \({R}_0\leq 1\).
Remarque 1. D'après la section 1, la reproductivité pour le système (2) est le rayon spectral de l' opérateur intégral \[u(t) \mapsto A(t) \int_0^\infty C(t,t-x)\, u(t-x)\, dx\] sur l'espace des fonctions continues périodiques, de période T, à valeurs dans \(\mathbb{R}^m\). Cet opérateur étant linéaire par rapport à \(A(t)\). Le système \[\frac{dJ}{dt} = (A(t)/{R}_0-B(t))J(t)\] a une reproductivité égale à 1, autrement dit, le multiplicateur de Floquet dominant est égal à 1. Ceci donne une méthode numérique pour calculer la reproductivité. Elle a été utilisée par (Bacaër, 2007, §3.4, §4.2, §5.1) pour plusieurs modèles particuliers tels que les modèles SEIR et les modèles de maladies à vecteurs, puis généralisée par (Wang et Zhao, 2008).
Remarque 2. Ayant déjà remarqué le rôle du transposé du système (2), mentionnons le lien entre \({R}_0\) et un problème de Sturm-Liouville du premier ordre. Considérons le système \(dV/dt=-B(t)V(t)\) avec la condition au bord \(V(0)=V(T)\). En suivant (Roseau, 1997), la fonction de Green associée est donnée par \[G(t,s)=\left \{\begin{array}{lll} Z(t) [I-Z(T)]^{-1} Z(s)^{-1} & , & 0\leq s < t \leq T,\\ Z(t) [I-Z(T)]^{-1} Z(T) Z(s)^{-1} & , & 0\leq t < s \leq T, \end{array}\right. \] comme chez (Bacaër, 2007, §2). Rappelons que \(dZ/dt=-B(t)Z(t)\) et \(Z(0)=\mathbb{I}\). Les solutions du problème différentiel de valeur propre \[\frac{dW}{dt}+B(t)W(t)=\lambda\, A(t) W(t),\quad W(0)=W(T)\] sont données par les solutions du problème intégral de valeur propre \[W(t) = \lambda \int_0^T G(t,s) A(s) W(s)\, ds.\] La valeur propre principale de ce problème est \(\lambda=1/{R}_0\) (cf. Bacaër et Ait Dads (2012) et Thieme (2009)).
Considérons un modèle SEIR linéarisé pour le début d'une épidémie: \begin{align} \frac{dE}{dt}&= -(b+ \mu) E + a(t) (1-\phi)\, I \tag{11}\\ \frac{dI}{dt}&= b\, E -(c+\mu) I \tag{12}. \end{align} Un tel modèle a été étudié par exemple par Dietz (1976).
Toutes les hypothèses de la section 2 sont satisfaites avec \begin{equation}\tag{13} A(t)=\left (\begin{array}{ccc} 0 && a(t) (1-\phi)\\ 0 && 0 \end{array}\right ),\quad B(t)= \left (\begin{array}{ccc} b+\mu && 0\\ -b && c+\mu \end{array}\right ). \end{equation} On calcule approximativement la probabilité d'extinction ω du processus de naissance et de mort &avec plusieurs types, associé avec (13), en partant de la condition initiale entière \((E(t_0),I(t_0))\neq (0,0)\). On choisit d'abord τ tel que \(\tau-t_0\) soit très grand comparé à T. On sait d'après (6), (7) et (8) que \begin{equation}\tag{14} \omega \simeq p(\tau,0,0)= \left (1-Y_1^{(\tau)}(\tau-t_0)\right )^{E(t_0)} \left (1-Y_2^{(\tau)}(\tau-t_0)\right )^{I(t_0)}, \end{equation} avec \begin{align} \frac{dY_1^{(\tau)}}{ds}(s) &= -(b+\mu) Y_1^{(\tau)}(s) + b\, Y_2^{(\tau)}(s),\tag{15}\\ \frac{dY_2^{(\tau)}}{ds}(s) &= a(\tau-s)\, (1-\phi) Y_1^{(\tau)}(s) (1-Y_2^{(\tau)}(s)) -(c+\mu) Y_2^{(\tau)}(s).\tag{16} \end{align} si \(0 < s < \tau-t_0\), \[Y_1^{(\tau)}(0)=1,\quad Y_2^{(\tau)}(0)=1.\] Ces équations permettent de calculer ω. Enfin on doit réutiliser le même algorithme avec une valeur plus grande de τ pour vérifier que la valeur approchée de ω est bien indépendante du choix de τ, pourvu que sa première valeur ait été choisie suffisamment grande.
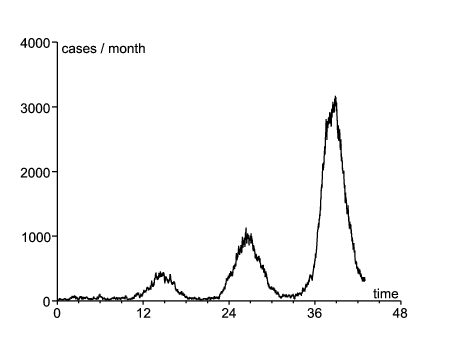
Comme exemple, considérons l'épidémie réémergente de rougeole en France durant les années 2008-2011 (figure 1 ; en 2006 et 2007 il y eut moins de 50 cas rapportés). En 2007, étant donnée la couverture vaccinale, on estime qu'environ 10% des enfants de deux ans et 7% des enfants de six ans en France pouvaient attraper la rougeole (Parent du Châtelet et coll., 2010, p. 4). En 2009-2010 environ 8% de la population âgée de 6 à 29 ans était susceptible (Lepoutre et coll., 2011, p. 5). Étant donnée la population totale de la France (65 millions d'habitants), on peut estimer que la population à risque est supérieure à deux millions de personnes. Par ailleurs, le nombre cumulé de cas rapportés dans la figure 1 est d'environ 22000, le nombre véritable de cas étant en certains lieux estimé être double de celui rapporté (Parent du Châtelet et coll., 2010, p. 3). Donc la population susceptible est probablement restée relativement stable durant les années 2008-2011, ce qui justifie le modèle linéarisé (11)-(12).

Supposons pour simplifier que \(a(t)=\bar{a} (1 + \varepsilon \cos (\omega t - \psi))\) avec \(\omega=2\pi/T\) et \(T=1\) an. Cette expression est le début du développement en série de Fourier de la fonction périodique \(a(t)\). D'autres formes pour \(a(t)\), comme la fonction en escalier (Keeling et Rohani, 2008), pourraient aussi être utilisées. Le forçage en escalier serait particulièrement approprié si une étude stratifiée par âge des cas indiquait une transmission à l'école. Cependant ceci ne semble pas être le cas. L'incidence la plus élevée est parmi les enfants de moins d'un an, qui ne sont pas encore scolarisés. L'âge médian des cas rapportés est 14 ans en 2010 et 16 ans en 2011, mais la plupart des cas ont moins de 30 ans (Baudon et coll., 2011). L'âge médian est ainsi particulièrement élevé pour une maladie telle que la rougeole. La structure par âge de l'incidence reflète en réalité la structure par âge de la population susceptible plus que la scolarisation. Les enfants de moins d'un an ne sont pas encore vaccinés. Comme indiqué ci-dessus, environ 8% de ceux âgés de 1 à 30 ans sont susceptibles; seulement 1 à 2% de ceux âgés de 30 à 50 ans sont susceptibles (Lepoutre et coll., 2011). Cette structure particulière est due au déclin rapide de l'incidence de la rougeole durant les années 1980 suite à la recommandation du vaccin contre la rougeole en 1983 et du vaccin ROR (rougeole, oreillons, rubéole) en 1986.
Pour estimer les paramètres inconnus, on compare le modèle déterministe (11)-(12), qui correspond à l'espérance du processus stochastique associé à (13), avec les données entre le début de janvier 2008 et juillet 2011. Des mesures sanitaires ont été prises alors pour contrôler l'épidémie. Les paramètres ne peuvent plus être supposés les mêmes qu'auparavant. Leur effet se voit à l'absence de vague épidémique à la fin de 2011.
On suppose \(1/b=8\) jours et \(1/c=5\) jours comme dans le §3.2.2.1 de (Keeling et Rohani, 2008). La mortalité μ est négligeable, comparée à b et c : on prend \(1/\mu=70\) ans. Soit f la fraction des cas qui sont véritablement rapportés. On identifie l'incidence des cas rapportés de la figure 1 avec la fonction \(f\, c\, I(t)\). Le système (11)-(12) étant linéaire, il est aussi vérifié par les fonctions \(\tilde{E}(t)=f\, E(t)\) et \(\tilde{I}(t)=f\, I(t)\). L'objectif est donc de trouver \(\tilde{E}(t^*)\), \(\tilde{I}(t^*)\), \(\varepsilon\), \(\psi\) et le produit \(\bar{a}(1-\phi)\) afin que \(c\, \tilde{I}(t)\) s'ajuste au mieux aux données. On mesure la distance aux données par la somme des valeurs absolues des différences d'incidence mensuelle. Ceci tend à donner un poids plus grand à la vague de 2011 à cause de sa taille. De toute façon les chiffres pour 2008 et 2009 sont petits et quelque peu irréguliers, probablement parce que plusieurs épidémies locales furent déclenchées par l'introduction de cas en provenance de l'étranger. On ne peut espérer un bon ajustement avec le modèle déterministe pour cette partie de la courbe épidémique, qui n'a pas encore atteint sa forme « stable » (au sens de la théorie des populations stables de Lotka). Quant à la vague de 2010, son pic a été atteint un mois plus tard que dans la vague de 2011. Ce décalage peut être dû à la stochasticité démographique ou au fait que \(a(t)\) n'est pas réellement périodique à cause de la stochasticité environnementale. À ces remarques près, on trouve un ajustement relativement bon (au moins pour la vague de 2011), étant donné la simplicité du modèle, avec \begin{equation}\tag{17} \tilde{E}(t^*)=3,\quad \tilde{I}(t^*)=2,\quad \varepsilon=\mbox{0,33}\, ,\quad \frac{\psi}{2\pi}=-\mbox{0,07}\, ,\quad \bar{a}(1-\phi)=\mbox{6,42}/\mathrm{mois} \end{equation} (figure 1).
En utilisant ces valeurs de paramètres, on peut simuler le processus de naissance et de mort. La figure 1 ne montre que l'espérance du nombre de cas par mois. Dans la version stochastique, l'épidémie s'éteint dans beaucoup de simulations. La figure 2 montre une simulation où l'épidémie ne s'est pas éteinte et où la taille des différentes vagues était du même ordre que les données de la figure 1 (des dizaines de simulations ont été nécessaires avant de trouver un tel exemple).
On garde la notation \({R}_0\) pour le cas où \(\phi=0\). D'après (Bacaër, 2007, §3.4), la reproductivité \({R}_\phi\) est caracterisée par le fait que le système linéaire périodique \begin{equation}\tag{18} \frac{dJ}{dt} = \left ( \begin{array}{ccc} -(b+\mu) & &a(t)(1-\phi) /{R}_\phi \\ b &&-(c+\mu) \end{array} \right ) J \end{equation} a un multiplicateur de Floquet dominant égal à 1. Numériquement on obtient \({R}_\phi\simeq \mbox{1,06}\). Noter que \({R}_\phi\) est seulement légèrement supérieur à 1. C'est parce que 90% de la population totale est déjà protégée, soit par vaccination, soit par une précédente infection.
On note d'ailleurs que le système (18) avec \(a(t)\) sinusoïdal peut être transformé en l'équation différentielle de Mathieu de la physique mathématique, comme dans le modèle de population étudié par Mingari Scarpello et Ritelli (2008).
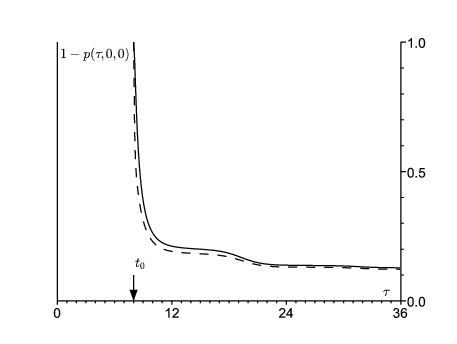
En utilisant les équations (14)-(16), on peut calculer la probabilité \(1-p(\tau,0,0)\) que le processus ne soit pas éteint au temps τ ( \(\tau\geq t_0\)). On part soit d'une personne dans le compartiment E, soit d'une personne dans le compartiment \(I\) (figure 3). Comme prévu, \(1-p(\tau,0,0)\) converge vers une limite 1−ω si \(\tau\to +\infty\). D'après la figure 3, l'extinction a le plus de chance d'avoir lieu pendant la première année après la date initiale.
En choisissant τ suffisamment grand et en répétant les calculs pour différentes valeurs de \(t_0\), on obtient la figure 4 pour la probabilité 1−ω que le processus de s'éteigne pas. On part soit d'un personne dans le compartiment E, soit d'une personne dans le compartiment \(I\). Cette probabilité est la plus élevée en septembre. C'est peut-être la période de l'année où les autorités sanitaires devraient faire le plus attention aux épidémies locales de rougeole pour agir le plus vite possible avant qu'elles ne déclenchent une épidémie majeure. À d'autres périodes de l'année, les épidémies ont plus de chance de s'éteindre par elles mêmes, même si \({R}_\phi>1\).
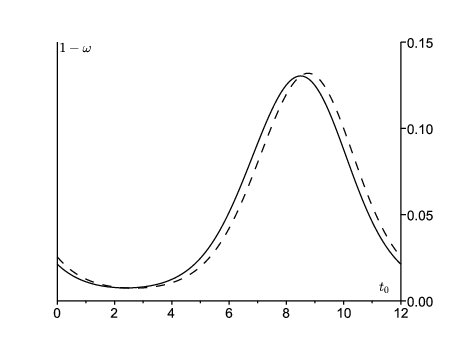
Noter que le pic d'incidence pour la vague de 2011 a eu lieu en mars 2011 (figure 1). L'estimation pour ψ suggère que le taux effectif de contacts \(a(t)\) a atteint son pic en décembre 2010. Le fond du creux entre les vagues de 2010 et 2011 est en août ou septembre 2010, à la saison où l'estimation de 1-ω est la plus haute. Si l'on avait utilisé principalement la vague de 2010 pour l'ajustement des paramètres, le pic pour 1-ω n'aurait été décalé que d'environ un mois. Donc quelle que soit la méthode, 1-ω semble être au plus haut plus ou moins quand l'incidence est au plus bas et le rebond de l'incidence démarre.
Bien entendu, il faut garder à l'esprit que ce modèle SEIR linearisé est une représentation par trop simplifiée de la dynamique de transmission de la rougeole. En particulier, il ne prend pas en compte la structure par âge et utilise un forçage saisonnier des contacts très simple.
D'autres domaines de la biologie des populations utilisent des processus de branchement, en particulier la biologie de la conservation (Caswell, 2001). Imaginons par exemple qu'une espèce animale qui est éteinte dans une certaine région soit réintroduite par les humains. Combien d'animaux faut-il réintroduire pour que la population ait une bonne chance de persister? Avec un processus de naissance et de mort pour un seul type d'animal, la probabilité d'extinction pour une population de n animaux est \(\omega^n\), où ω est donné par (1). Connaissant ω, on peut donc estimer n tel que \(\omega^n\) soit inférieur à un certain niveau de risque. Bien sûr, la réintroduction n'a de sens que dans les cas où ω < 1, pour lesquels \(\omega^n\) peut être rendu petit en choisissant n assez grand. Une autre question se pose: à quel moment de l'année les animaux doivent-ils être réintroduits de manière à minimiser la probabilité d'extinction ω ? La même question se pose dans le cadre des processus de naissance et de mort à plusieurs types dans un environnement périodique, avec la possibilité supplémentaire de demander quel type d'individu doit être réintroduit pour minimiser la probabilité d'extinction.
Alors que les modèles en temps continu sont très populaires en épidémiologie, les biologistes de la conservation tendent à préférer les modèles en temps discret pour diverses raisons. Dans le reste de cette sous-section, on explique brièvement comment des probabilités d'extinction se calculent dans ce contexte. La justification du lien entre \(R_0\) et la probabilité d'extinction est en fait bien plus simple dans le cas du temps discret que dans celui du temps continu de la section 2. Il découle de méthodes connues
Considérons les modèles en temps discret \[p(t+1)=(A(t)+B(t))p(t).\] \(A(t)\) et \(B(t)\) sont des matrices carrés de taille m, à coefficients positifs ou nuls. On suppose
Pour la version stochastique correspondante, on doit spécifier les probabilités \(F^{(j)}_{k_1,\ldots,k_m}(t)\) qu'un individu de type j donne naissance à \(k_1\) individus de type 1, … , \(k_m\) individus de type m, entre les temps t et t+1. Les fonctions \(F^{(j)}_{k_1,\ldots,k_m}(t)\) sont des fonctions périodiques de période T par rapport à t. Alors \[A_{ij}(t)=\sum_{k_1,\ldots,k_m} k_i \, F^{(j)}_{k_1,\ldots,k_m}(t).\] Le coefficient \(B_{ij}(t)\) donne la probabilité pour qu'un individu de type j soit transféré vers le type i entre t et t+1. Un individu de type j au temps t est remplacé au temps t+1 par une population dont la fonction génératrice est \[g_j(t,x_1,\ldots,x_m)=\Bigl ( \sum_{k_1,\ldots,k_m}\!\!\! F^{(j)}_{k_1,\ldots,k_m}(t)\, x_1^{k_1}\cdots x_m^{k_m}\Bigr ) \Bigl (1 + \sum_i B_{ij}(t) (x_i-1) \Bigr ).\] Entre les instants \(t_0\) et \(t_0+T\), un individu de type j est remplacé par une population dont la fonction génératrice \(h_j(x_1,\ldots,x_m)\) est obtenue en composant les fonctions génératrices \(g_j(t,x_1,\ldots,x_m)\) avec \(t=t_0,\ldots,t_0+T-1\). Si par exemple \(\ T=2\), \[h_j(x_1,\ldots,x_m)=g_j(t_0,g_1(t_0+1,x_1,\ldots,x_m),\ldots,g_m(t_0+1,x_1,\ldots,x_m)).\]
Considérons les instants \((t_0+nT)_{n\geq 0}\). On sait d'après la théorie des processus de branchement à plusieurs types dans un environnement constant que les probabilités d'extinction \(\omega_j\) partant d'un individu de type j au temps \(t_0\) sont la solution minimale sur \([0,1]^m\) du système \[\omega_j=h_j(\omega_1,\ldots,\omega_m),\quad 1\leq j\leq m.\] On a \[\frac{\partial g_j}{\partial x_i}(t,1,\ldots,1)=A_{ij}(t)+B_{ij}(t).\] La matrice des moyennes, c'est-à-dire la matrice jacobienne en (1,…,1), est \[\left (\frac{\partial h_j}{\partial x_i}(1,\ldots,1)\right )_{i,j}=(A(t_0+T-1)+B(t_0+T-1))\cdots (A(t_0)+B(t_0)).\] On suppose que cette matrice de moyennes est primitive et que les fonctions génératrices \(h_j\) ne sont pas singulières, c'est-à-dire qu'il n'y ait pas de matrice Q telle que \[h_j(x_1,\ldots,x_m)=\sum_k Q_{jk}\, x_k,\quad \forall j.\] Le théorème 2 d'Athreya et Ney (1972, p. 186) montre que \((\omega_1,\ldots,\omega_m)=(1,\ldots,1)\) si et seulement si le rayon spectral de cette matrice des moyennes est inférieur ou égal à 1. Ceci est équivalent à \(R_0\leq 1\), et
Comme exemple, considérons un modèle avec un seul type d'animal, \(p(t+1)=(A(t)+B(t))p(t)\), avec \(T=2\ \). On suppose que chaque individu donne naissance entre les temps t et t+1 à une progéniture selon une distribution de Poisson. La moyenne est \(A(t)\). Alors \begin{align*} g(0,x)&=e^{A(0)(x-1)}\, (1-B(0)+B(0)x),\\ g(1,x)&=e^{A(1)(x-1)}\, (1-B(1)+B(1)x). \end{align*} La probabilité d'extinction partant d'un invidividu au temps 0 est la plus petite solution de \[\omega=g(0,g(1,\omega)),\quad \omega \in [0,1].\] De même, la probabilité d'extinction partant d'un individu au temps 1 est la plus petite solution de \[\omega=g(1,g(0,\omega)),\quad \omega \in [0,1].\] Ces deux probabilités sont strictement inférieures à 1 si \[(A(1)+B(1))(A(0)+B(0)) > 1.\] Ceci équivaut à \(R_0 > 1\). \(R_0\) est le rayon spectral de \[\left ( \begin{array}{cc} A(0) & 0 \\ 0 & A(1) \end{array} \right ) \left ( \begin{array}{cc} -B(0) & 1 \\ 1 & -B(1) \end{array} \right )^{-1}.\]
Des travaux ont essayé de montrer comment le risque épidémique varie dans différents mois de l'année. Ils ont utilisé un modèle périodique. Ils ont calculé une « reproductivité » \(R(t_0)\), en supposant les coefficients du modèle gelés. Ils ont dessiné \(R(t_0)\) en fonction de \(t_0\) (Hartemink et coll., 2009). Le problème avec cette méthode est que \(R(t_0)\) peut être inférieur à 1 tout le temps, tandis que la maladie devient endémique.
La définition de la reproductivité utilisée dans notre article détermine bien si une maladie infectieuse peut être endémique (Rebelo et coll., 2012) et comment la taille finale se comporte dans les modèles épidémiques (Bacaër et Gomes, 2009). De plus elle a une interprétation biologique simple comme taux asymptotique de croissance par generation (Bacaër et Ait Dads, 2011 ; Bacaër et Ait Dads, 2012). Mais elle a le désavantage apparent d'être indépendante du temps. Un autre indice de risque épidémique, ayant le bon seuil et qui est périodique, a été proposé récemment par (Cushing et Ackleh, 2011). Mais son interpretation biologique semble un peu compliquée.
Ici on a calculé une mesure alternative du risque épidémique, la probabilité que le processus de branchement associé à la linéarisation d'un modèle épidémique ne s'éteigne pas. Sa principale propriété mathématique est le phénomène de seuil (proposition de la section 2). (Bacaër, 2007, §5.2) avait déjà suggéré d'utiliser cette probabilité pour des applications en épidémiologie mais n'avait considéré que le cas de populations à un seul type, pour lesquelles il existe une formule explicite. La plupart des modèles épidémiques font intervenir plusieurs compartiments infectés comme par exemple dans le cas des maladies à vecteurs. Le risque épidémique dans de tels modèles peut être analysé avec la même méthode numérique que dans la figure 2.
Les probabilités d'extinction intéressent aussi la biologie de la conservation, en particulier pour la réintroduction d'espèces. Pour certaines espèces animales, en particulier pour les oiseaux avec une période de nidification bien définie, il serait peut-être judicieux d'utiliser des modèles avec des saisons pour évaluer correctement la chance de succès d'une réintroduction.