Numerization of a memory effect for an homogenized composite material with a large contrast in the phase thermal conductivities
Résumé
In this article, we propose a systematic numerical solution method for deriving the homogenized material parameters in the case where a large contrast in the phase thermal properties leads to a macroscopic memory effect. Focus is therefore set on the determination of this memory effect for a periodic microstructure. As for other and more classical homogenized parameters, the possibility of analyzing with the finite element method a single periodic cell is used, and a transient simulation allows to provide the incremental evolution of the memory effect function. Additionally, some approximations are proposed for a low cost estimate of this function, and validated on two examples.
|
|---|
Fichier principal
preprint.pdf (846.56 Ko)
Télécharger le fichier
cell2F_new.gif (4.35 Mo)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |
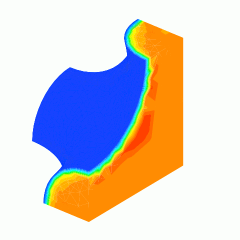
| Commentaire | Homogenization of a micro-structured material with a large contrast in conductivity properties: numerical determination of a memory effect. Homogenization methods allow the multiscale modelling of heterogeneous materials possessing a microstructure. More precisely, they lead to the determination of averaged macroscopic properties. When the microstructure is largely heterogeneous, the macroscopic model may change in nature. Herein, a thermal problem with a large contrast in conductivity leads to a non-locality in time (memory effect). The associated material properties can also be determined with a transient periodic computation on a small scale cell. This picture illustrates this back in time transient solution on one phase of the microstructure. |
Loading...